Die wederkerige of wederkerige is baie handig in allerhande algebraïese vergelykings. Byvoorbeeld, as u een breuk deur 'n ander deel, vermenigvuldig u die eerste breuk met die wederkerige van die tweede. U moet ook die inverse gebruik as u die vergelyking van 'n lyn soek.
Stap
Metode 1 van 3: vind die omgekeerde van 'n breuk of heelgetal
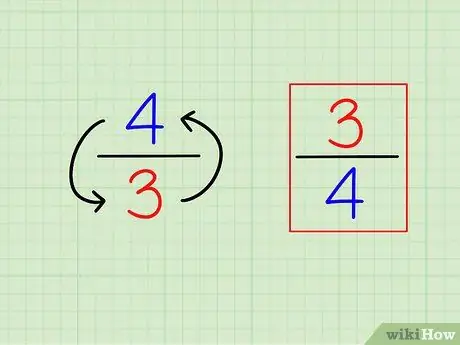
Stap 1. Vind die wederkerigheid van die breuk deur dit om te keer
Die definisie van "wederkerig" of die teenoorgestelde is baie maklik. Om die wederkerigheid van enige heelgetal te vind, bereken eenvoudig "1 (daardie getal)". Vir breuke is die wedersydse 'n ander breuk, dit wil sê, die getalle is "omgekeerd" (omgekeerd).
- Byvoorbeeld, die teenoorgestelde van 3/4 is 4/3.
- Enige getal vermenigvuldig met sy wedersydse opbrengste 1.
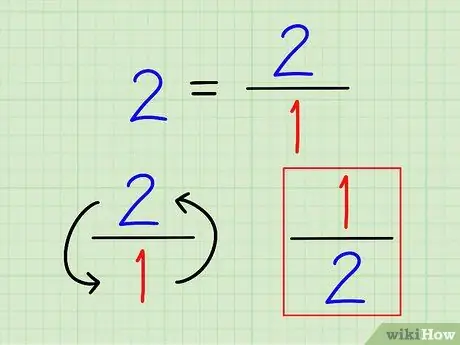
Stap 2. Skryf die wederkerigheid van die heelgetal as 'n breuk neer
Weereens, die wedersydse van 'n getal is altyd 1 (daardie getal). Vir heelgetalle, skryf dit as breuke. Daar is geen sin om die getal tot 'n desimale te bereken nie.
Byvoorbeeld, die wederkerige van 2 is 1 2 = 1/2.
Metode 2 van 3: vind die omgekeerde van 'n gemengde breuk
Stap 1. Identifiseer gemengde getalle
Gemengde breuke bestaan uit heelgetalle en breuke, soos 24/5. Daar is twee stappe om die wederkerigheid van 'n gemengde getal te vind, soos hieronder beskryf.
Stap 2. Skakel gemengde getalle om in onbehoorlike breuke
Onthou dat 1 altyd as (getal)/(dieselfde getal) geskryf kan word, en breuke met dieselfde noemer (onderste getal) kan bymekaargetel word. Hier is 'n voorbeeld van 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
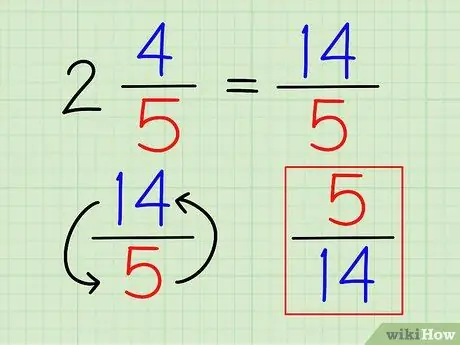
Stap 3. Draai die breuk om
Sodra die getal volledig as 'n breuk geskryf is, kan u die wederkerigheid vind, net soos met enige ander breuk, deur die breuk om te keer.
In die voorbeeld hierbo is die wedersydse van 14/5 is 5/14.
Metode 3 van 3: Vind die teenoorgestelde van 'n desimaal
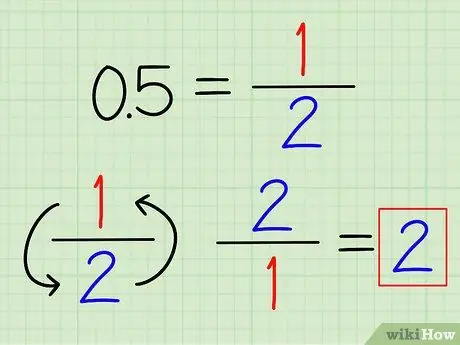
Stap 1. Omskakel desimale as breuke indien moontlik
U herken moontlik 'n paar desimale getalle wat gereeld gebruik word, wat maklik in breuke omgeskakel kan word. Byvoorbeeld, 0,5 = 1/2 en 0,25 = 1/4. Sodra die desimaal in 'n breuk omgeskakel is, draai die breuk eenvoudig om sy wederkerigheid te vind.
Byvoorbeeld, die wederkerige van 0,5 is 2/1 = 2.
Stap 2. Skryf 'n delingsprobleem
As u dit nie in 'n breuk kan omskakel nie, bereken die wederkerigheid van die getal in die vorm van 'n delingsprobleem: 1 (desimaal). U kan 'n sakrekenaar gebruik om dit op te los, of gaan voort met die volgende stap om dit met die hand op te los.
U kan byvoorbeeld die wederkerige van 0,4 vind deur 1 0,4 te bereken
Stap 3. Verander die delingsprobleem om heelgetalle te gebruik
Die eerste stap om desimale te verdeel, is om die desimale punt te skuif totdat al die getalle heelgetalle is. Solank u die desimale punt van beide getalle met dieselfde aantal stappe skuif, kry u die regte antwoord.
U kan byvoorbeeld 1 0, 4 gebruik en dit herskryf as 10 4. In hierdie geval skuif u al die desimale plekke een stap na regs, op dieselfde manier as wat u elke getal met tien vermenigvuldig
Stap 4. Los die probleem op met lang afdeling
Gebruik die langverdelingmetode om die wedersydse te bereken. As jy 10 4 tel, kry jy die antwoord 2, 5 wat die wederkerige van 0, 4 is.
Wenke
- Die negatiewe wederkerigheid van 'n getal is dieselfde as die gewone wederkerige, deurdat dit vermenigvuldig word met negatiewe getal. Byvoorbeeld, die negatiewe wedersydse van 3/4 is -4/3.
- Daar word dikwels na die wedersydse of wederkerige verwys as die "vermenigvuldiging inverse".
- Die getal 1 is die teenoorgestelde van homself omdat 1 1 = 1.
- Die getal 0 het geen wederkerigheid nie, want 0 is ongedefinieerd.
