- Outeur Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:11.
- Laas verander 2025-01-23 12:05.
Aftrek is eenvoudig die aftrekking van een getal van die ander. Dit is maklik om een heel getal van 'n ander af te trek, maar aftrekking kan lastig wees as u breuke of desimale aftrek. Sodra u aftrekking verstaan, kan u meer ingewikkelde wiskundige konsepte gebruik en getalle makliker byvoeg, vermenigvuldig en verdeel.
Stap
Metode 1 van 6: Trek groot getalle af deur te leen

Stap 1. Skryf 'n groot getal neer
Byvoorbeeld, jy wil 32 - 17. los. Skryf eers 32 neer.

Stap 2. Skryf die kleiner getal reg onder dit neer
Maak seker dat u die tiene en ene waardes in die korrekte kolomme plaas, sodat 3 van 32 direk bo 1 van 17 en 2 van 32 direk bo 7 van 17 is.
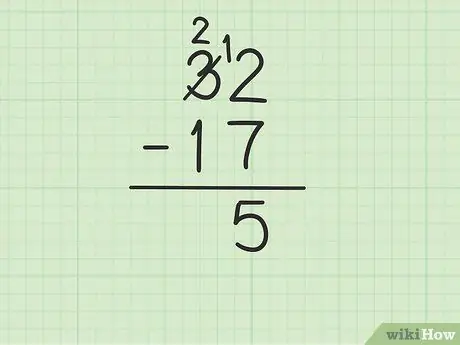
Stap 3. Trek die boonste nommer in die kolom eenhede af van die getal onderaan
Dit kan egter ingewikkeld raak as die onderste getal groter is as die boonste getal. In hierdie geval is 7 groter as 2. Hier is wat u moet doen:
- U moet leen by die nommer 3 van 32 (ook bekend as groepering) om 2 in 12 te verander.
- Kruis die nommer 3 uit 32 en vervang dit met die getal 2, terwyl die getal 2 12 word.
- Nou kan u 12 - 7 aftrek, wat gelyk is aan 5. Skryf 5 onder die twee getalle wat u aftrek, sodat dit in die eenheidskolom van die nuwe ry is.
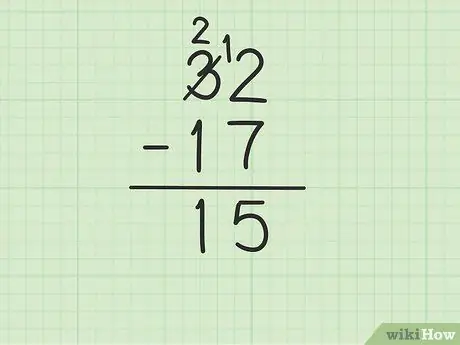
Stap 4. Trek die boonste getal in die kolom tiene van die onderste getal af
Onthou dat 3 geword het 2. Trek nou 1 van 17 af van 2 hierbo om (2-1) te kry 1. Skryf 1 hieronder, in die tiene kolom, links van 5 in die eenheidskolom. Jy skryf 15. Dit wil sê, 32 - 17 = 15.
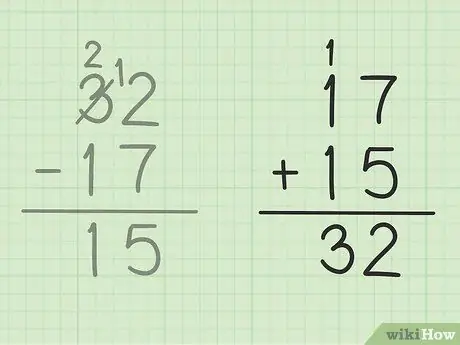
Stap 5. Gaan u werk na
As u wil seker maak dat u twee getalle korrek afgetrek het, hoef u net u antwoord met die kleiner getal by te voeg om 'n groot getal te maak. In hierdie probleem moet u u antwoord, 15 by die kleiner aantal aftrekking, 17. 15 + 17 = 32, byvoeg sodat u antwoord korrek is. Veilig!
Metode 2 van 6: Trek klein getalle af
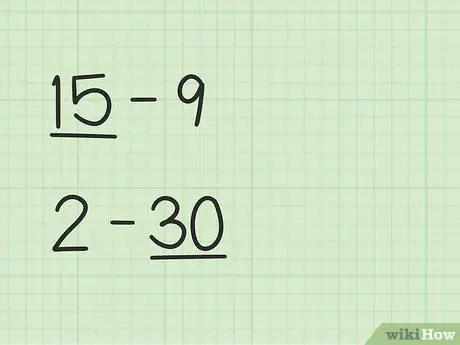
Stap 1. Vind die groter getal
Probleme soos 15 -9 het 'n ander manier as 2 -30.
- In vrae 15 - 9 is die eerste getal, 15, groter as die tweede getal, 9.
- In vrae 2 - 30 is die tweede getal, 30, groter as die eerste getal, 2.
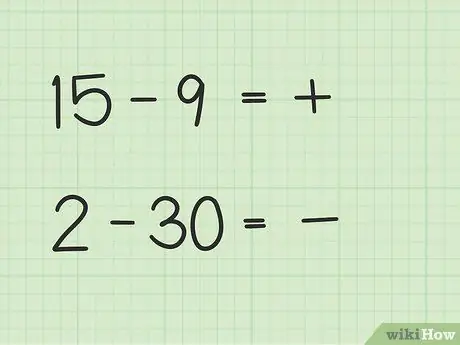
Stap 2. Besluit of u antwoord positief of negatief sal wees
As die eerste getal groter is, is die antwoord positief. As die tweede getal groter is, is die antwoord negatief.
- In die eerste vraag, 15 - 9, is u antwoord positief, want die eerste getal is groter as die tweede getal.
- In die tweede vraag, 2 - 30, is u antwoord negatief omdat die tweede getal groter is as die eerste getal.
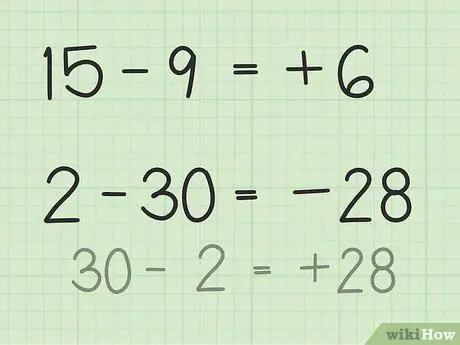
Stap 3. Vind die verskil tussen twee getalle
Om twee getalle af te trek, moet u die verskil tussen die twee getalle voorstel en die getalle tussen hulle bereken.
- By vrae 15 - 9, stel u 'n stapel 15 poker chips voor. Gooi 9 skyfies weg en slegs 6. Dus, 15 - 9 = 6. U kan u ook 'n getallelyn voorstel. Dink aan die nommers van 1 tot 15, gooi dan 9 eenhede weg of gee dit terug sodat jy 6 kry.
- Vir vrae 2 - 30 is die maklikste manier om dit op te los, die getal om te keer en die resultaat negatief te maak na aftrek. Dus, 30 - 2 = 28 so 28 en 30 het 'n verskil van 2. Maak nou die resultaat negatief omdat u reeds bepaal het dat die antwoord negatief is omdat die tweede getal groter is as die eerste getal. Dus, 2 -30 = -28.
Metode 3 van 6: Trek desimale af
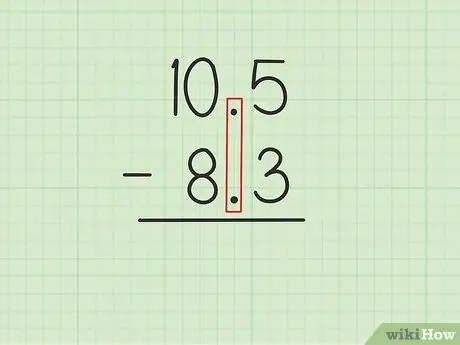
Stap 1. Skryf die groter getal oor die kleiner getal met die desimale punte in lyn
Gestel jy wil die volgende probleme oplos: 10, 5 - 8, 3. Skryf 10, 5 oor 8, 3 sodat die desimale punte van die twee getalle ewewydig is., 5 van 10, 5 moet direk bo, 3 van 8, 3 en 0 van 10, 5 moet bo 8 van 8, 3 wees.
As u 'n probleem ondervind omdat die twee getalle nie dieselfde getal na die desimale punt het nie, skryf 0 in die spasie totdat die som van die getalle dieselfde is. Die probleem is byvoorbeeld 5, 32 - 4, 2, u kan dit as 5, 32 - 4, 2 skryf 0. Dit sal nie die waarde van die tweede getal verander nie, maar dit sal dit makliker maak om die twee getalle af te trek.

Stap 2. Trek die boonste getal in die kolom tiene van die getal hieronder af
In hierdie geval moet u 3 aftrek van 5. 5 - 3 = 2, dus moet u 2 onder 3 van 8, 3 skryf.
Maak seker dat u 'n desimale punt in die antwoord plaas, sodat dit geskryf word, 2

Stap 3. Trek die getal bo die kolom eenhede af van die getal daaronder
U moet 8 van 0. aftrek. Leen 1 uit die tiene om 0 na 10 te verander en 10 - 8 af te trek om 2. U kan ook 10 - 8 tel sonder om te leen, want daar is geen getalle in die tweede tiene kolom nie. Skryf die antwoord onder 8, links van die desimale punt.

Stap 4. Skryf u finale uitslag neer
U uiteindelike resultaat is 2, 2.

Stap 5. Gaan jou werk na
As u wil seker maak dat u desimale aftrekking korrek is, hoef u net u antwoord met die kleiner getal by te voeg om die groter getal te maak. 2, 2 + 8, 3 = 10, 5, so jy is klaar.
Metode 4 van 6: Trek breuke af

Stap 1. Rig die noemer en teller van die breuk in lyn
Gestel u wil probleme oplos 13/10 - 3/5. Skryf die probleem neer sodat die twee tellers, 13 en 3 en die twee noemers, 10 en 5 teenoor mekaar is. Hierdie twee getalle word geskei deur 'n aftrekkingsteken. Dit sal u help om die probleem te visualiseer en makliker op te los.

Stap 2. Vind die minste gemene deler
Die minste gemene deler is die kleinste getal wat deur twee getalle gedeel kan word. In hierdie voorbeeld moet u die kleinste gemene deler vind wat deelbaar is met 10 en 5. U vind dat 10 die kleinste gemene deler vir beide getalle is, want 10 is deelbaar met 10 en 5.
Let daarop dat die minste gemene deler van twee getalle nie altyd een daarvan is nie. Die kleinste gemene deler vir 3 en 2 is byvoorbeeld 6 omdat 6 die kleinste getal is wat deur twee getalle gedeel kan word
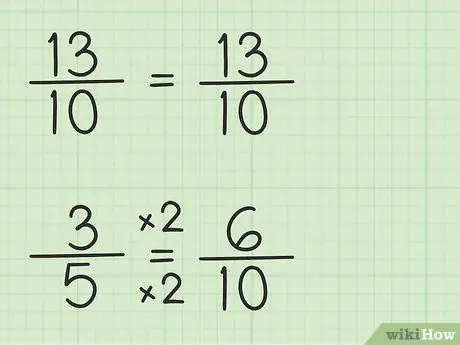
Stap 3. Skryf die breuke neer met dieselfde noemer
Die breuk 13/10 kan op dieselfde manier geskryf word omdat die noemer 10 is, die kleinste gemene deler, wat 10 is, maal 1. Die breuk 3/5 moet egter herskryf word omdat die noemer 5 is, die kleinste gemene deler, wat 10 is, maal 2. Dus moet die breuk 3/5 met 2/2 vermenigvuldig word om die noemer 10 te maak, dus 3/5 x 2/2 = 6/10. U het die ekwivalente breuk gevind. 3/5 is gelykstaande aan 6/10, hoewel 6/10 u toelaat om die eerste getal, 13/10, af te trek.
Skryf 'n nuwe vraag soos volg: 13/10 - 6/10
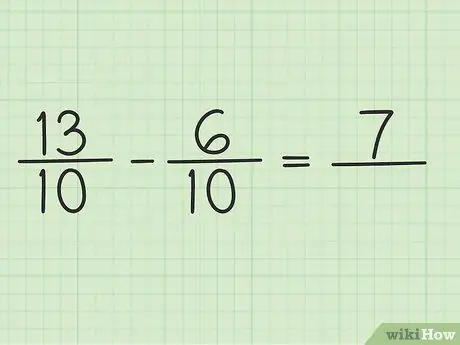
Stap 4. Trek die teller af op twee getalle
Trek net 13 - 6 af, sodat die resultaat 7 is. U kan nie die noemer van die breuk verander nie.
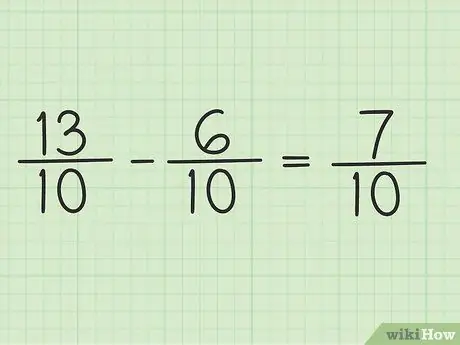
Stap 5. Skryf die nuwe teller oor dieselfde noemer om die finale uitslag te kry
Die nuwe teller is 7. Beide breuke het 'n noemer van 10. U finale resultaat is 7/10.
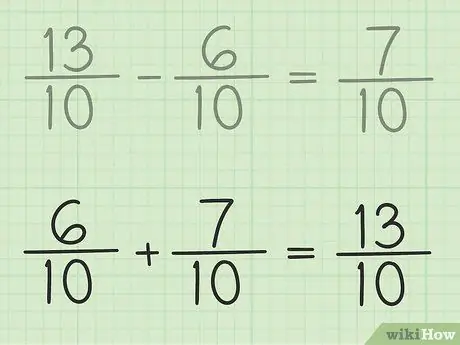
Stap 6. Gaan u werk na
As u wil seker maak dat u die breuk korrek aftrek, tel u u antwoord en die kleiner breuk op, sodat die resultaat 'n groter breuk is. 7/10 + 6/10 = 13/10. Dit is klaar.
Metode 5 van 6: Trek breuke van heelgetalle af

Stap 1. Skryf die probleem neer
Gestel u wil byvoorbeeld die volgende probleem oplos: 5 -. Skryf dit neer.
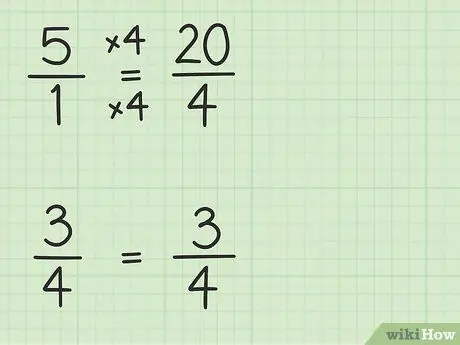
Stap 2. Skakel heelgetalle om in breuke met dieselfde noemer as ander breuke
U sal 5 in 'n breuk omskakel met 'n noemer van 4 om twee getalle af te trek. U moet dus aan 5 dink as 'n breukdeel van 5/1. Dan kan u die teller en noemer van die nuwe breuk met 4 vermenigvuldig om die noemers van die twee getalle dieselfde te maak. Dus 5/1 x 4/4 = 20/4. Hierdie breuk is gelyk aan 5, maar laat jou toe om twee getalle af te trek.
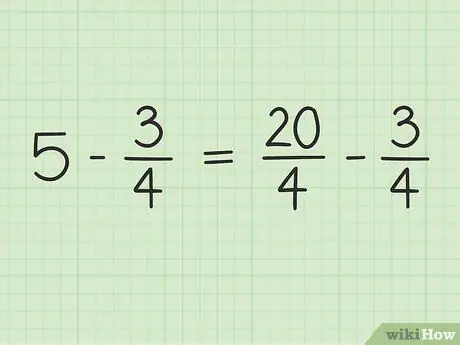
Stap 3. Skryf die probleem oor
Die nuwe probleem kan so geskryf word: 20/4 - 3/4.
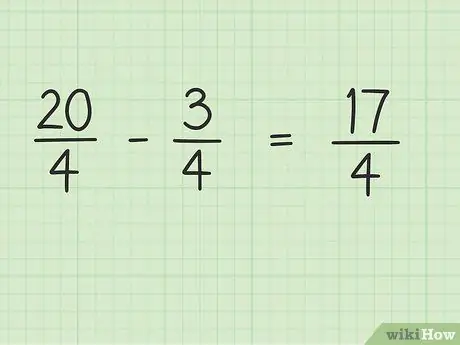
Stap 4. Trek die teller van die breuk af, terwyl die noemer dieselfde bly
Trek nou 20 by 3 af om die finale uitslag te kry. 20 - 3 = 17, dus 17 is die nuwe teller. U kan die noemer dieselfde laat.
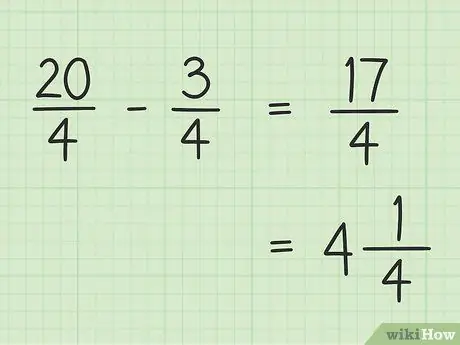
Stap 5. Skryf u finale uitslag neer
U finale uitslag is 17/4. As jy dit as 'n gemengde getal wil skryf, deel 17 met 4 sodat die resultaat 4 is en die res 1, sodat jou laaste 17/4 gelyk is aan 4.
Metode 6 van 6: Trek veranderlikes af
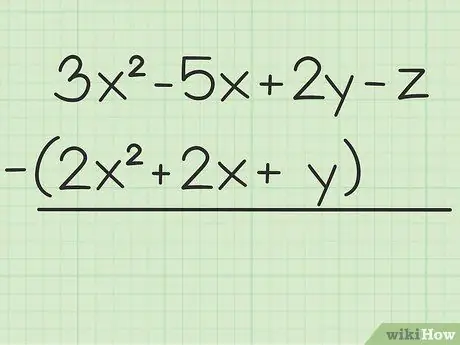
Stap 1. Skryf die probleem neer wat u wil oplos
Byvoorbeeld die volgende vraag: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Skryf die eerste stel veranderlikes oor die tweede.
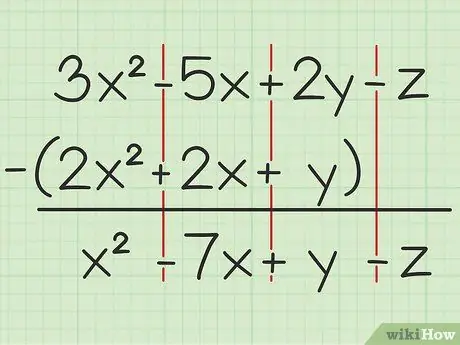
Stap 2. Trek dieselfde veranderlikes af
As u 'n veranderlike teëkom, kan u slegs dieselfde veranderlike optel of aftrek en wat met dieselfde kwadraat geskryf is. Dit beteken dat u 4x kan aftrek2 van 7x2, maar kan nie 4x van 4y aftrek nie. U kan die probleem dus soos volg verdeel:
- 3x2 - 2x2 = x2
- -5x -2x = -7x
- 2y - y = y
- -z -0 = -z
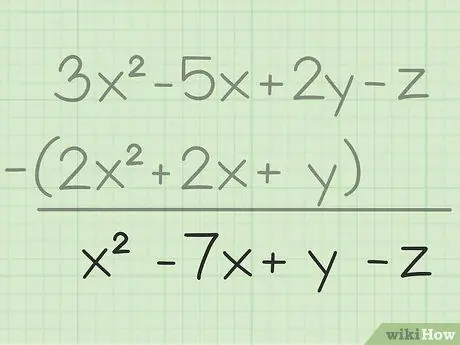
Stap 3. Skryf u finale uitslag neer
U het dieselfde veranderlikes afgetrek; u hoef slegs u finale resultaat te skryf, wat al die veranderlikes bevat wat u afgetrek het. Hier is die eindresultaat:






