Hoe om lensvergroting te bereken: 12 stappe (met foto's)

2024 Outeur: Jason Gerald | [email protected]. Laas verander: 2024-01-16 19:05

By die bestudering van optiese instrumente is die "vergroting" van 'n lensagtige voorwerp die verhouding tussen die hoogte van die beeld wat u sien en die werklike hoogte van die voorwerp. Byvoorbeeld, 'n lens wat 'n voorwerp baie groot kan laat lyk, het 'n "hoë" vergrotingsfaktor, terwyl 'n lens wat 'n voorwerp klein laat lyk, 'n "lae" vergrotingsfaktor het. Die formule vir die vergroting van 'n voorwerp word gewoonlik met behulp van die formule bereken M = (h_ek/h_o) = -(d_ek/d_o), waar M = vergroting, h_ek = beeldhoogte, h_o = hoogte van voorwerp, en d_ek en D._o = afstand van beeld en voorwerp.

Stap

Metode 1 van 2: Berekening van enkel lens vergroting

Notas: A. konvergerende lens breër in die middel as aan die rande (soos 'n vergrootglas). a uiteenlopende lens wyer aan die kante as in die middel (soos 'n bak). Die berekening van die vergroting op beide lense is dieselfde, met een belangrike uitsondering. Klik hier om direk na die uitsonderings op uiteenlopende lense te gaan.

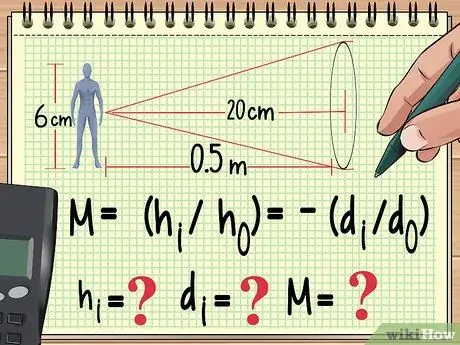
Stap 1. Begin met u vergelyking en die veranderlikes wat u reeds ken

Net soos enige ander fisika -probleem, is die manier om 'n vergrotingsprobleem op te los, deur die vergelyking neer te skryf wat u sal gebruik om dit te bereken. Van hieruit kan u agteruit werk om die waarde van die veranderlike wat u nie gevind het nie, te vind uit die vergelyking wat u gebruik.

• Gestel byvoorbeeld dat 'n pop van 6 cm 'n meter van 'n meter af geplaas word konvergerende lens met 'n brandpuntsafstand van 20 cm. As ons die vergroting, beeldhoogte en beeldafstand wil bereken, kan ons ons vergelyking soos volg begin skryf:

  M = (h_ek/h_o) = -(d_ek/d_o)

• Nou weet ons h_o (hoogte van die pop) en d_o (poppeafstand van lens). Ons ken ook die brandpunt van die lens, wat nie in hierdie vergelyking is nie. Ons sal tel h_ek, d_ek, en M..

Stap 2. Gebruik die lensvergelyking om d te kry_ek.

As u die afstand van die voorwerp wat u vergroot en die brandpuntsafstand van die lens ken, is dit baie maklik om die afstand van die gevormde beeld te bereken met die lensvergelyking. Die vergelyking van die lens is 1/f = 1/d_o + 1/d_ek, waar f = brandpunt van die lens.

• In hierdie voorbeeldprobleem kan ons die lensvergelyking gebruik om d te bereken_ek. Voer die waardes van f en d in_ek los dan die vergelyking op:

  1/f = 1/d_o + 1/d_ek

  1/20 = 1/50 + 1/d_ek

  5/100 - 2/100 = 1/d_ek

  3/100 = 1/d_ek

  100/3 = d_ek = 33,3 cm

• Die brandpuntsafstand van die lens is die afstand van die middel van die lens tot die punt waar lig by die fokuspunt oorgedra word. As jy ooit lig met 'n vergrootglas op brandende miere gefokus het, het jy dit gesien. In die vrae in die les is die grootte van hierdie hotspot gewoonlik gegee. In die werklike lewe word hierdie spesifikasies gewoonlik op 'n etiket op die lens geskryf.

Stap 3. Berekening van h_ek.

Nadat u d bereken het_o en D._ek, kan u die hoogte van die vergrote voorwerp en die vergroting van die lens bereken. Let op die twee gelyke tekens in die vergrootglasvergelyking (M = (h_ek/h_o) = -(d_ek/d_o)) - dit beteken dat alle dele van hierdie vergelyking gelyk is aan mekaar, sodat ons M en h kan bereken_ek in watter volgorde ons ook al wil.

• Vir hierdie voorbeeldprobleem kan ons h bereken_ek soos hierdie:

  (h_ek/h_o) = -(d_ek/d_o)

  (h_ek/6) = -(33, 3/50)

  h_ek = -(33, 3/50) x 6

  h_ek = - 3,996 cm

• Let daarop dat die hoogte van die voorwerp hier negatief is, wat aandui dat die prentjie wat ons later sal sien, omgekeerd (bo-onder) sal wees.

Stap 4. Berekening van M

U kan die laaste veranderlike bereken met die vergelyking -(d_ek/d_o) of (h_ek/h_o).

• In die volgende voorbeeld is die berekening van M soos volg:

  M = (h_ek/h_o)

  M = (-3, 996/6) = - 0, 666

• Die resultaat sal ook dieselfde wees as dit bereken word met die waarde van d:

  M = -(d_ek/d_o)

  M = -(33, 3/50) = - 0, 666

• Let daarop dat die zoom nie 'n eenheidsetiket het nie.

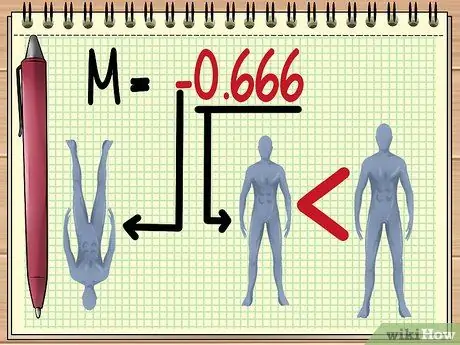
Stap 5. Verstaan die M -waarde

Sodra u die grootte van die M -waarde gekry het, kan u 'n paar dinge skat oor die beeld wat u deur die lens sal sien, naamlik:

• Die grootte.

  Hoe groter die "absolute waarde" van M, hoe groter sal die voorwerp wat met die lens bekyk word, verskyn. M -waarde tussen 0 tot 1 dui aan dat die voorwerp kleiner sal lyk.

• Voorwerporiëntasie.

  'N Negatiewe waarde dui aan dat die gevormde beeld omgekeer sal word.

• In die voorbeeld wat hier gegee word, beteken die M -waarde van -0.666 dat die skaduwee van die pop sigbaar sal wees volgens die waarde van die bestaande veranderlike. onderstebo en twee derdes kleiner as die werklike grootte.

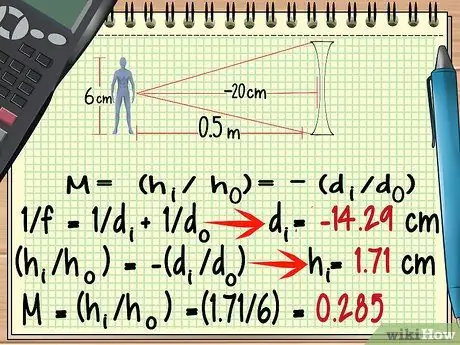
Stap 6. Gebruik 'n negatiewe fokuspunt vir 'n uiteenlopende lens

Alhoewel die vorm van 'n divergerende lens baie anders is as die van 'n konvergerende lens, kan u die vergroting daarvan bereken met dieselfde formule as hierbo. Die uitsonderings om in gedagte te hou is Die fokuspunt van die divergerende lens is negatief.

In die voorbeeldprobleem hierbo beïnvloed dit die antwoord wat u sal kry by die berekening van d_ek, so maak seker dat u hieraan aandag gee.

• Laat ons die voorbeeldprobleem hierbo herwerk, maar nou gebruik ons 'n uiteenlopende lens met brandpuntsafstand - 20 cm.

  Die ander veranderlikes bly dieselfde waarde.

• In die eerste plek bereken ons d_ek met behulp van die lensvergelyking:

  1/f = 1/d_o + 1/d_ek

  1/-20 = 1/50 + 1/d_ek

  -5/100 - 2/100 = 1/d_ek

  -7/100 = 1/d_ek

  -100/7 = d_ek = - 14, 29 cm

• Nou sal ons h bereken_ek en M met die waarde van d_ek die nuwe een.

  (h_ek/h_o) = -(d_ek/d_o)

  (h_ek/6) = -(-14, 29/50)

  h_ek = -(-14, 29/50) x 6

  h_ek = 1,71 cm

  M = (h_ek/h_o)

  M = (1, 71/6) = 0, 285

Metode 2 van 2: Berekening van die vergroting van veelvuldige lense

Eenvoudige twee lens metode

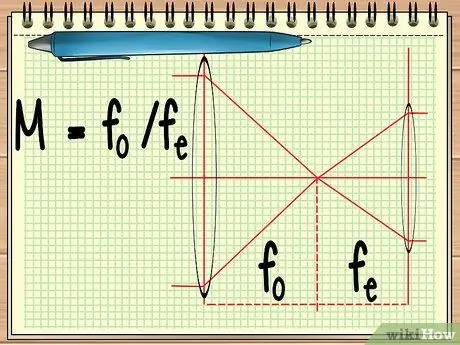
Stap 1. Bereken die fokuspunt van die twee lense

As u 'n instrument gebruik wat bestaan uit twee lense wat langs mekaar gerangskik is (soos 'n teleskoop of 'n verkyker), is dit net die fokuspunt van die twee lense om die algehele vergroting van die twee lense te bereken. dit kan bereken word deur die eenvoudige vergelyking M = f_o/f_e.

In die vergelyking, f_o is die fokuspunt van die objektiewe lens en f_e is die fokuspunt van die oogstuk. Die objektieflens is die groot lens wat naby die voorwerp is, terwyl die ooglens die lens is wat naby die oog van die waarnemer geleë is.

Stap 2. Koppel die inligting wat u reeds het in die vergelyking M = f_o/f_e.

Sodra u die fokuspunte van albei lense het, is dit baie maklik om dit te bereken, - bereken die verhouding deur die brandpuntsafstand van die objektiewe lens te deel deur die brandpuntsafstand van die okular. Die antwoord wat u kry, is die totale vergroting van die instrument.

• Gestel byvoorbeeld 'n eenvoudige teleskoop, daar word geskryf dat die fokuspunt van die objektief 10cm is en die fokuspunt van die oogstuk 5cm, dan is die vergroting 10/5 = 2.

  Ingewikkelde metode

  

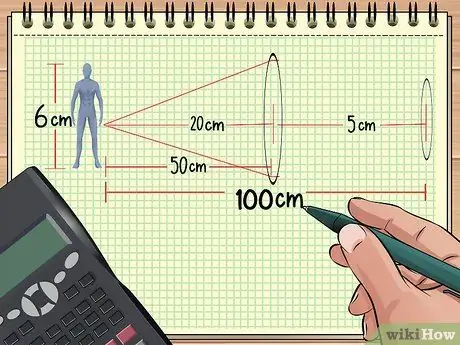
  Stap 1. Bereken die afstand tussen die lense en die voorwerp

  As u twee lense in 'n ry voor 'n voorwerp gerangskik het, kan die totale vergroting bereken word as u die afstand van die lense tot die voorwerp, die grootte van die voorwerp en die fokuspunt van die twee lense ken. Die res kan ook bereken word.

  Gestel ons rangskik byvoorbeeld voorwerpe en lense soos in voorbeeld 1 hierbo: 'n pop is 50 cm van 'n konvergerende lens met 'n brandpunt van 20 cm. Plaas nou die tweede lens met 'n fokuspunt van 5 cm op 'n afstand van 50 cm van die eerste lens (100 cm van die pop af). Daarna bereken ons die totale vergroting met behulp van die inligting wat ons gekry het

  

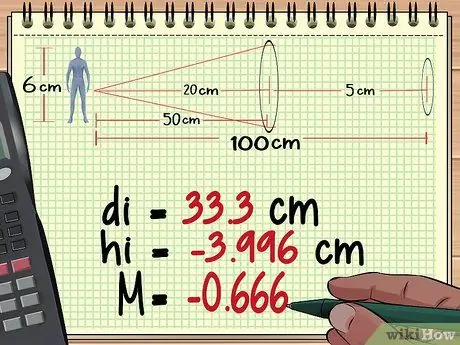
  Stap 2. Bereken die voorwerpafstand, hoogte en vergroting vanaf lens 1

  Die eerste deel van die berekening van die vergroting van veelvuldige lense is dieselfde as die berekening van die vergroting van 'n enkele lens. Begin met die lens naaste aan die voorwerp, gebruik die lensvergelyking om die afstand van die gevormde beeld te bepaal, en gebruik dan die vergrotingsvergelyking om die hoogte en vergroting van die beeld te bepaal. Klik hier om meer enkel lens vergroting berekeninge te sien.

  • Uit ons berekeninge in metode 1 hierbo, vind ons dat die eerste lens 'n beeld van so hoog as - 3,996 cm, afstand 33,3 cm agter die lens, en met 'n vergroting van - 0, 666.

    

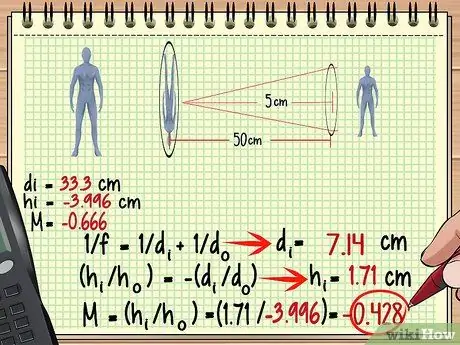
    Stap 3. Gebruik die beeld van die eerste lens as die voorwerp van die tweede lens

    Dit is nou baie maklik om die vergroting, hoogte en meer vir die tweede lens te vind - gebruik net dieselfde metode as wat u vir die eerste lens gebruik het, maar behandel die beeld hierdie keer as 'n voorwerp. Onthou dat die beeldafstand tot die tweede lens nie altyd dieselfde is as die voorwerpafstand tot die eerste lens nie.

    • In die voorbeeld hierbo, aangesien die beeld 33,3 cm agter die eerste lens gevorm word, is die afstand 50-33,3 = 16,7 cm voor die tweede lens. Kom ons gebruik hierdie meting en die brandpuntsafstand van die tweede lens om die beeld te vind wat deur die tweede lens gevorm word.

      1/f = 1/d_o + 1/d_ek

      1/5 = 1/16, 7 + 1/d_ek

      0, 2 - 0, 0599 = 1/d_ek

      0, 14 = 1/d_ek

      d_ek = 7,14 cm

    • Nou kan ons h bereken_ek en M vir die tweede lens:

      (h_ek/h_o) = -(d_ek/d_o)

      (h_ek/-3, 996) = -(7, 14/16, 7)

      h_ek = -(0, 427) x -3, 996

      h_ek = 1,71 cm

      M = (h_ek/h_o)

      M = (1, 71/-3, 996) = - 0, 428

    

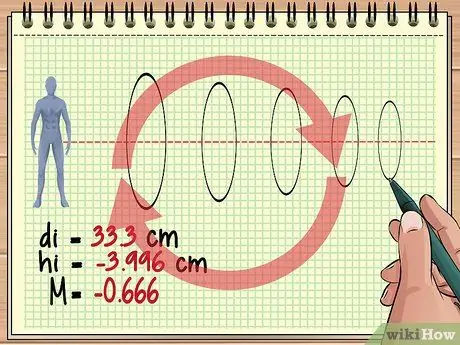
    Stap 4. Gaan voort om so te bereken vir die ekstra lense

    Hierdie basiese benadering is dieselfde as daar drie, vier of honderde lense voor 'n voorwerp staan. Beskou vir elke lens die beeld van die vorige lens as die voorwerp en gebruik die lensvergelyking en die vergrotingsvergelyking om die antwoord te vind wat u wil hê.

    Hou in gedagte dat elke daaropvolgende lens die gevormde beeld voortdurend kan omkeer. Die vergrotingswaarde wat ons vroeër verkry het (-0, 428) dui byvoorbeeld aan dat die beeld wat ons gaan sien ongeveer 4/10 van die werklike voorwerpgrootte is, maar loodreg, omdat die beeld van die vorige lens omgekeerd is

    Wenke

    • Verrekykers gee gewoonlik 'n verduideliking van die vergrotingspesifikasies in die vorm van 'n getal maal 'n ander getal. 'N Verkyker kan byvoorbeeld as 8x25 of 8x40 gespesifiseer word. As dit so geskryf word, is die eerste getal die vergroting van die verkyker. Dit maak nie saak nie, selfs al is die twee getalle in die voorbeeld verskil, beide verkykers het 'n vergroting van 8 keer. Die tweede nommer dui aan hoe duidelik die beeld deur die verkyker gevorm sal word.
    • Onthou dat die vergroting negatief sal wees as 'n enkellensloep as die voorwerpafstand groter is as die brandpunt van die lens. Dit beteken nie dat die gevormde beeld kleiner sal wees nie. In hierdie geval vind die vergroting steeds plaas, maar die gevormde beeld sal deur die waarnemer onderstebo (bo-na onder) gesien word.