- Outeur Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Laas verander 2025-01-23 12:05.
Die vierkantswortel van 'n getal is maklik om te vind as die antwoord 'n heelgetal is. As die antwoord nie 'n heelgetal is nie, is daar 'n reeks prosesse wat u kan volg om die vierkantswortel te kry, selfs al gebruik u nie 'n sakrekenaar nie. Hiervoor moet u die basiese beginsels van vermenigvuldiging, optelling en deling verstaan.
Stap
Metode 1 van 3: Soek die vierkantswortel van 'n heelgetal
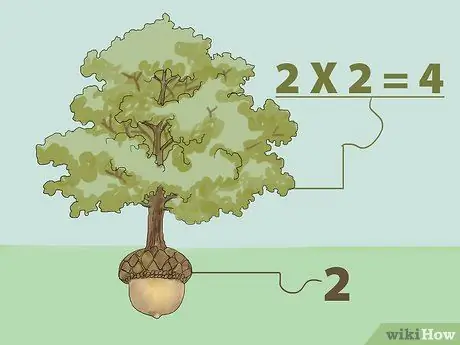
Stap 1. Vind die perfekte vierkantswortel deur te vermenigvuldig
Die vierkantswortel van 'n getal is 'n getal wat, as dit met homself vermenigvuldig word, die oorspronklike getal terugbring. Met ander woorde: "Watter getal kan ons op sigself vermenigvuldig om die getal te kry wat ons wil hê?"
- Byvoorbeeld, die vierkantswortel van 1 is 1 omdat 1 vermenigvuldig met 1 1 is (1X1 = 1). Die vierkantswortel van 4 is dus 2 omdat 2 vermenigvuldig met 2 4 is (2X2 = 4). Beskou die vierkantswortelkonsep as 'n boom. 'N Boom groei uit saad. Dus, 'n boom is groter as 'n saad, wat groei uit 'n saad wat sy wortel is. Uit die voorbeeld hierbo is 4 die boom en 2 is die saad.
- Dus, die vierkantswortel van 9 is 3 (3X3 = 9), van 16 is 4 (4X4 = 16), van 25 is 5 (5X5 = 25), van 36 is 6 (6X6 = 36), van 49 is 7 (7X7 = 49), van 64 is 8 (8X8 = 64), van 81 is 9 (9X9 = 81) en van 100 is 10 (10X10 = 100).
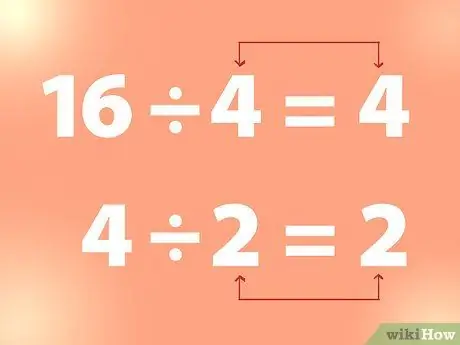
Stap 2. Gebruik deurlopende verdeling om die vierkantswortel te vind
Om die vierkantswortel van 'n heelgetal te vind, kan jy die heelgetal deur 'n getal deel totdat jy 'n getal kry wat gelyk is aan die deler.
- Voorbeeld: 16 gedeel deur 4 is 4. En 4 gedeel deur 2 is 2, ensovoorts. Uit die voorbeeld hierbo is 4 dus die vierkantswortel van 16 en 2 is die vierkantswortel van 4.
- Perfekte vierkantswortels het geen breuke of desimale nie, want dit is heelgetalle.
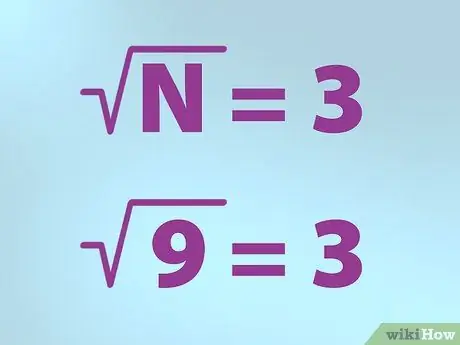
Stap 3. Gebruik die korrekte simbool vir die vierkantswortel
Wiskundiges gebruik 'n spesiale simbool om die vierkantswortel voor te stel. Die vorm is soos 'n regmerkie met 'n lyn regs bo.
- N is gelyk aan die getal waarvoor u die vierkantswortel wil vind. N word onder die vinkje geplaas.
- Dus, as u die vierkantswortel van 9 wil vind, skryf 'n formule deur "N" (9) binne 'n vinkje te plaas (simbool "wortel"), skryf dan 'n gelyke teken en gevolg deur 3. Dit beteken "vierkantswortel van 9 is gelyk aan 3 ".
Metode 2 van 3: Soek die vierkantswortel van 'n ander getal
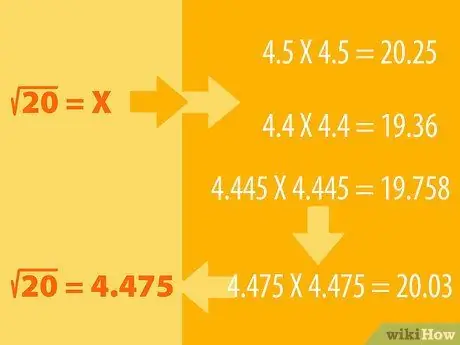
Stap 1. Raai, en doen die proses van eliminasie
Dit is moeilik om die vierkantswortel van 'n nie-heelgetal te vind. Dit beteken egter nie dat dit onmoontlik is nie.
- Sê byvoorbeeld dat u die vierkantswortel van 20. wil vind. Ons weet dat 16 'n volmaakte vierkant is waarvan die vierkantswortel 4 is (4X4 = 16). Dan is die 25 vierkantswortels 5 (5X5 = 25), dus moet die vierkantswortel van 20 tussen die twee lê.
- U kan raai dat die vierkantswortel van 20. 4.5 is. Nou vierkant 4.5 om die resultaat te sien. Dit wil sê, ons vermenigvuldig 4, 5 op sigself: 4, 5X4, 5. Kyk of die antwoord min of meer as 20. As u raaiskoot te ver is, probeer 'n ander getal (bv. 4, 6 of 4, 4) en pas aan die raai dienooreenkomstig. totdat u die nommer 20 kry.
- Byvoorbeeld, 4, 5X4, 5 = 20, 25, so logies moet ons 'n kleiner getal vind, miskien 4, 4. 4, 4X4, 4 = 19, 36. Die vierkantswortel van 20 moet dus tussen 4, 5 en 4, 4. Probeer met 4, 445X4, 445. Die resultaat is 19, 758. Die resultaat kom al hoe nader. Hou aan om met ander getalle te probeer totdat u 4, 475X4, 475 = 20, 03 kry. Afgerond, die getal is gelyk aan 20.

Stap 2. Gebruik die gemiddelde proses
Hierdie proses begin ook deur die twee naaste volmaakte vierkante te vind wat omring word deur die getal.
- Verdeel die getal dan met een van die perfekte vierkantswortels. Neem die antwoord en vind die gemiddelde tussen die getal en die getal waarvan u die wortel wil vind (u kan die gemiddelde vind deur die twee bymekaar te tel en deur twee te deel). Verdeel dan die aanvanklike getal deur die gemiddelde wat verkry is. Die laaste stap, vind die gemiddelde van die resultate met die gemiddelde wat die eerste keer bereken is.
- Klink dit ingewikkeld? Dit sou makliker wees as 'n voorbeeld gegee word. Byvoorbeeld, 10 lê tussen die twee perfekte vierkante 9 (3X3 = 9) en 16 (4X4 = 16). Die vierkantswortels van beide getalle is 3 en 4. Dus, deel 10 met die eerste getal, 3. Die resultaat is 3, 33. Vind nou die gemiddelde van 3 en 3, 33 deur hulle bymekaar te tel en te deel met 2. Die resultaat is 3, 1667 Deel nou 10 met 3.1667. Die resultaat is 3.1579. Vind dan die gemiddelde van 3.1579 en 3.1667 deur hulle op te tel en te deel met 2. Die resultaat is 3.1623.
- Kontroleer u resultaat deur die antwoord (in hierdie voorbeeld 3, 1623) self te vermenigvuldig. Die resultaat van 3.1623 vermenigvuldig met 3.1623 blyk 10.001 te wees.
Metode 3 van 3: Negatiewe getalle kwadraat
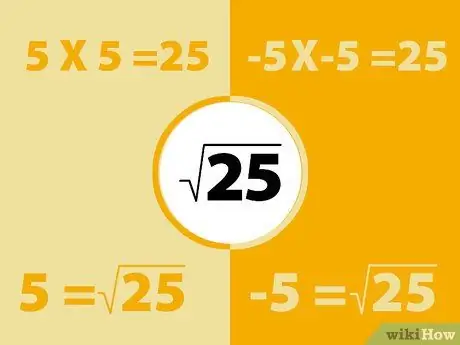
Stap 1. Vierkantige negatiewe getalle met dieselfde metode
Onthou dat negatiewe tye negatief positief is. Die kwadraat van 'n negatiewe getal sal dus 'n positiewe getal lewer.
- Byvoorbeeld, -5X -5 = 25. Onthou egter ook dat 5x5 = 25. Dus kan die vierkantswortel van 25 -5 of 5. wees. Basies het elke getal twee vierkantswortels.
- Net so is 3X3 = 9 en -3X -3 = 9, dus is die vierkantswortels van 9 3 en -3. Die positiewe vierkantswortel word die 'hoofwortel' genoem. Op hierdie stadium moet ons net aandag gee aan hierdie antwoord.
Stap 2. Gebruik 'n sakrekenaar
Alhoewel dit die beste is om die wiskunde met die hand te doen, is daar baie aanlyn sakrekenaars beskikbaar om vierkantswortels te bereken.
- Soek die vierkantswortelknoppie op 'n gewone sakrekenaar.
- Tik in die aanlyn sakrekenaar die nommer waarvoor u die vierkantswortelwaarde wil vind en klik op die knoppie. Die rekenaar wys die vierkantswortelwaarde.
Wenke
-
Hou altyd 'n paar belangrike perfekte vierkante in gedagte:
- 02 = 0, 12 = 1, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49, 82 = 64, 92 = 81, 102 = 100,
- Onthou ook hierdie perfekte vierkant: 112 = 121, 122 = 144, 132 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289…
- Let ook op hierdie: 102 = 100, 202 = 400, 302 = 900, 402 = 1600, 502 = 2500, …






