- Outeur Jason Gerald [email protected].
- Public 2024-01-15 08:08.
- Laas verander 2025-01-23 12:05.
In meganiese ingenieurswese is die ratverhouding 'n direkte meting van die rotasiesnelheid van twee of meer ratte wat kompeterend ingeskakel is. As 'n algemene reël vir twee ratte, as die aandrywing (die rat wat die draaikrag direk van die enjin, motor, ens. Ontvang) groter is as die aangedrewe rat, draai die aangedrewe rat vinniger en omgekeerd. Ons kan hierdie basiese konsep in 'n formule skryf Ratverhouding = T2/T1, T1 is die aantal tande in die eerste rat en T2 is die aantal tande in die tweede rat.
Stap
Metode 1 van 2: Berekening van ratverhouding in ratkring
Twee ratte
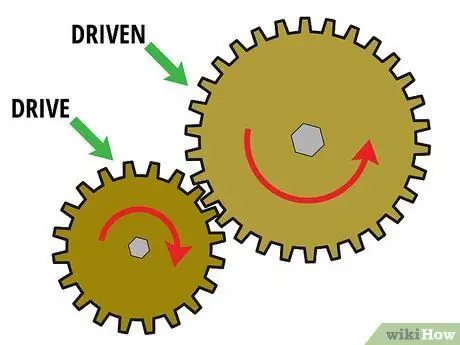
Stap 1. Begin met 'n stel met twee ratte
Ten einde die ratverhouding te bepaal, moet u ten minste twee ratte met mekaar verbind. Hierdie twee onderlinge ratte word "ratstelle" genoem. Oor die algemeen is die eerste rat 'n "aandrywing" wat op die motoras gemonteer is en die tweede rat is 'n "aangedrewe rat" wat op die lasas gemonteer is. 'N Aantal ratte kan ook tussenin teenwoordig wees om krag van die dryfrat na die aangedrewe rat oor te dra. Hierdie ratte word "ratte sonder vrag" genoem.
Kom ons kyk nou na 'n ratstel wat slegs twee ratte bevat. Om die ratverhouding te bereken, moet hierdie twee ratte met mekaar in wisselwerking tree. Met ander woorde, die tande moet maas en die een moet die ander draai. Gestel u het byvoorbeeld 'n klein dryfrat (rat 1) wat 'n groter rat (rat 2) draai
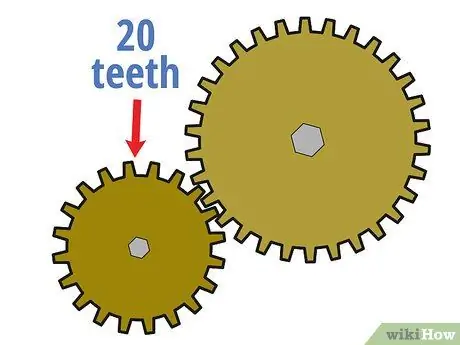
Stap 2. Tel die aantal tande op die dryfrat
Een manier om die ratverhouding tussen twee versnellingsratte te bereken, is om die aantal tande (klein tandagtige stampe aan die rand van die wiel) te vergelyk. Begin deur te tel hoeveel tande in die ratkas is. U kan dit doen deur handmatig of soms te bereken deur na die inligting op die aandrywing te kyk.
Gestel byvoorbeeld die kleiner dryfrat in die stelsel 20 tande.
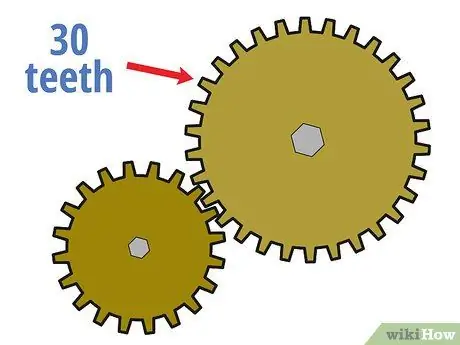
Stap 3. Tel die aantal tande op die aangedrewe rat
Tel dan hoeveel tande daar in die aangedrewe rat is, soos u voorheen vir die dryfrat gehad het.
Gestel die aangedrewe rat het byvoorbeeld 30 tande.
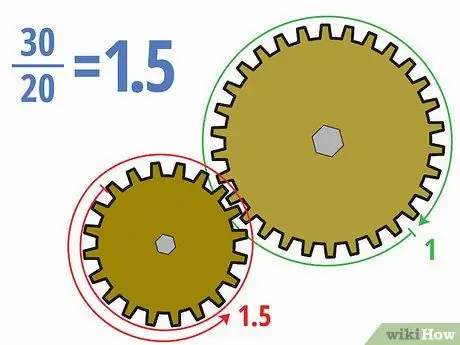
Stap 4. Verdeel die aantal tande met mekaar
Noudat u weet hoeveel tande in elke rat is, kan u die ratverhoudings redelik maklik bereken. Verdeel die tande op die aangedrewe rat deur die tande op die dryfrat. U kan die antwoord in desimale, breuke of verhoudingsvorm skryf (soos x: y), afhangende van u opdrag.
- In die voorbeeld hierbo gee 30/20 = 30 tande in die aangedrewe rat deur 20 tande in die aandrywing 1, 5. Ons kan dit ook inskryf 3/2 of 1, 5: 1.
- Die betekenis van hierdie ratverhouding is dat die kleiner aandrywing een en 'n half keer moet draai sodat die groter aangedrewe rat een volledige omwenteling kan maak. Omdat die aangedrewe rat groter is, sal die aangedrewe rat stadiger draai.
Meer as twee ratte
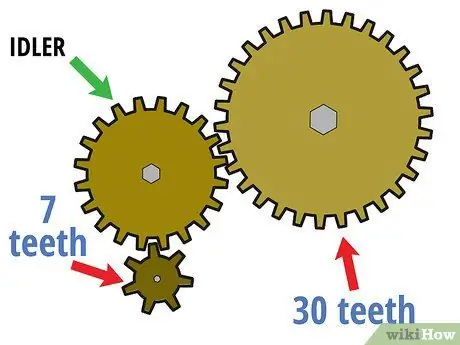
Stap 1. Begin met 'n ratstel wat meer as twee ratte het
Soos die naam aandui, kan 'n "ratstel" bestaan uit 'n lang reeks ratte, nie net een aandrywing en een aangedrewe rat nie. In hierdie geval bly die eerste rat die dryfrat, die laaste rat bly die aangedrewe rat, en die middelste rat word die "onbelaste rat". Hierdie onbelaaide ratte word dikwels gebruik om die draairigting te verander of om twee ratte aan te sluit wanneer direkte ratverstelling dit swaar of onbeskikbaar sou maak.
Veronderstel byvoorbeeld dat die bogenoemde tweegang-stroombaan nou aangedryf word deur 'n rat met sewe klein tande. In hierdie geval het die rat met 30 vaste tande die aangedrewe rat geword, en die rat met 20 tande (wat voorheen die aandrywing was) is nou die gelaaide rat
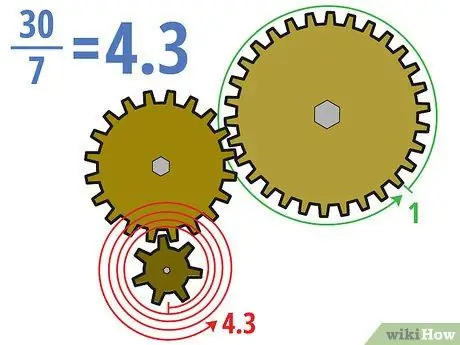
Stap 2. Verdeel die aantal tande van die aandrywing en die aangedrewe rat
Die belangrikste ding om te onthou wanneer u te doen het met ratstelle wat meer as twee ratte het, is dat slegs die aandrywing en die aangedrewe rat (gewoonlik die eerste en laaste rat) belangrik is. Met ander woorde, ratte sonder vrag beïnvloed glad nie die ratverhouding van die hele stel nie. Nadat u die aandrywing en die aangedrewe rat geïdentifiseer het, kan u die ratverhoudings dieselfde bereken as voorheen.
In die voorbeeld hierbo sal ons die ratverhouding bereken deur die dertig tande van die aangedrewe rat te deel deur die sewe tande van die nuwe aandrywing. 30/7 = ongeveer. 4, 3 (of 4, 3: 1). Dit beteken dat die aandrywing ongeveer 4,3 keer moet draai sodat die veel groter aangedrewe rat een keer kan draai.
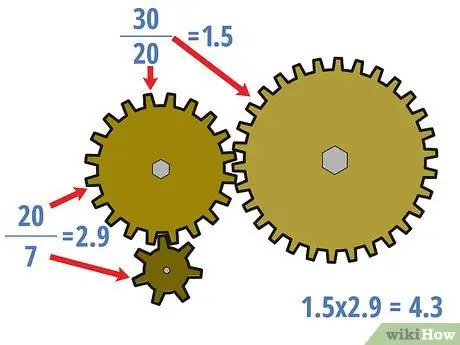
Stap 3. Bereken indien nodig die ratverhouding vir die middelrat
U kan die ratverhoudings wat onbelaaide ratte behels ook bereken, en u wil dit in sekere situasies doen. Begin in hierdie geval by die dryfrat en werk tot by die laairat. Behandel die vorige rat soos 'n dryfrat tot by die volgende rat. Verdeel die aantal tande op elke "aangedrewe" rat deur die aantal tande op die "aandrywing" vir elke stel versnellingsratte om die middelratverhouding te bereken.
- In die voorbeeld hierbo is die sentrale ratverhouding 20/7 = 2, 9 en 30/20 = 1, 5. Daar moet op gelet word dat hierdie verhoudings nie dieselfde is as die ratverhouding vir die hele stel nie, wat 4.3 is.
- Maar, moet ook op gelet word dat (20/7) × (30/20) = 4, 3. In die algemeen moet die verhoudings van die middelste ratte van die ratstel vermenigvuldig word om gelyk te wees aan die verhouding van alle ratte.
Metode 2 van 2: Berekening van verhoudings/spoed
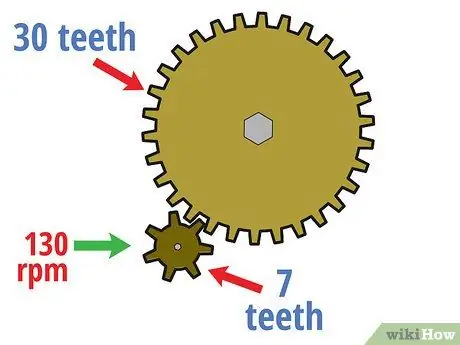
Stap 1. Bereken die rotasiesnelheid van die aandrywing
Deur die konsep van ratverhoudings te gebruik, is dit maklik om te bepaal hoe vinnig die aangedrewe rat draai op grond van die "inset" -snelheid van die dryfrat. Bereken eers die rotasiesnelheid van die aandrywing. In baie ratberekeninge lei dit tot omwentelinge per minuut (rpm), hoewel ander spoed -eenhede ook gebruik kan word.
Gestel byvoorbeeld in die voorbeeld van die ratkring hierbo met 'n dryfrat met sewe tande en 'n aangedrewe rat met 30 tande, draai die dryfrat teen 'n snelheid van 130 rpm. Met hierdie inligting, bereken ons die snelheid van die aangedrewe rat in die volgende stappe
Stap 2. Koppel hierdie inligting in die formule S1 × T1 = S2 × T2
In hierdie formule verwys S1 na die rotasiesnelheid van die aandrywing, T1 verwys na die tande van die aandrywing, en S2 en T2 verwys na die snelheid en tande van die aangedrewe rat. Vul hierdie veranderlikes in totdat u slegs een veranderlike oor het.
- Dikwels vind u in sulke vrae die grootte van S2, hoewel dit moontlik is om ander veranderlikes te vind. In die voorbeeld hierbo kry ons die volgende inligting:
- 130 rpm × 7 = S2 × 30
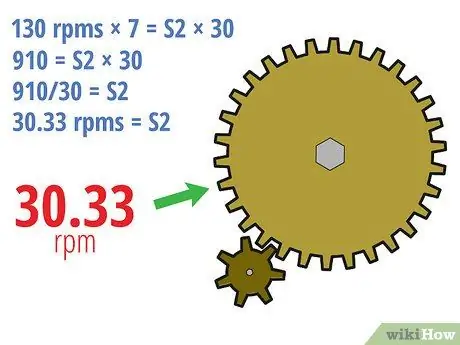
Stap 3. Voltooi
Die berekening van die oorblywende veranderlikes is slegs 'n basiese wiskundige probleem. Vereenvoudig die oorblywende vergelykings en isoleer die veranderlike aan die een kant van die vergelykingsteken, en u kry die antwoord. Moenie vergeet om dit in die korrekte eenhede te skryf nie. As gevolg hiervan kan u waarde uit huiswerk verloor.
- In die voorbeeld hierbo kan ons dit oplos deur:
- 130 rpm × 7 = S2 × 30
- 910 = S2 × 30
- 910/30 = S2
- 30, 33 rpm = S2
- Met ander woorde, as die dryfrat teen 'n snelheid van 130 rpm draai, sal die aangedrewe rat teen 'n snelheid van 30,33 rpm draai. Aangesien die aangedrewe rat baie groter is, sal die aangedrewe rat baie stadiger draai.
Wenke
- Om te sien hoe die ratverhouding -beginsel van toepassing is, probeer om met u fiets te ry. Let daarop dat die maklikste manier om te klim, is as u 'n klein rat aan die voorkant en 'n groot rat agterin het. Dit is makliker om die kleiner rat met die krag van die pedale te draai, maar die agterwiel moet baie draaie neem in vergelyking met die ratopstelling wat u vir plat oppervlaktes sou gebruik. Dit laat jou stadiger beweeg.
- 'N Afgradeerde stelsel (wanneer die laai -toerusting minder is as die motortoerental), benodig 'n motor wat optimale drywing lewer by hoër rotasiesnelhede.
- Die krag wat benodig word om die vrag aan te dryf, word deur die ratverhoudings van die motor verhoog of verlaag. Die grootte van hierdie motor moet verander word om die krag te verskaf wat die vrag benodig nadat die ratverhouding bereken is. 'N Verhoogde stelsel (wanneer die toerental van die las groter is as die motortoerental), benodig 'n motor wat optimale drywing lewer teen laer rotasiesnelhede.






