- Outeur Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:11.
- Laas verander 2025-01-23 12:05.
Almal kan Wiskunde leer, of hulle nou reeds op 'n hoër stadium op skool is of net weer die basiese beginsels wil slyp. Na 'n bespreking van hoe om 'n goeie leerder in wiskunde te wees, sal hierdie artikel u die basiese wiskundige vordering leer en gee u die basiese elemente wat u in elke oefening moet leer. Dan bespreek hierdie artikel die basiese beginsels van rekenkundige leer, wat beide laerskoolkinders en almal wat die basiese beginsels van hierdie veld wil leer, sal help.
Stap
Deel 1 van 6: Sleutels om 'n goeie wiskundestudent te word

Stap 1. Verskyn in die klas
As u die klas mis, moet u konsepte by klasmaats of uit u handboek leer. U kry nooit 'n teksopsomming van 'n vriend soos u van u onderwyser kry nie.
- Kom betyds klas toe. Kom eerder 'n bietjie vroeg en maak u notaboek op die regte plek oop, maak u handboek oop en haal u sakrekenaar uit sodat u gereed is om te begin as u onderwyser gereed is om te onderrig.
- Sê net as u siek is. As u die klas regtig mis, vra u klasmaats om uit te vind waaroor die onderwyser praat en watter huiswerk gegee is.

Stap 2. Werk saam met u onderwyser
As u onderwyser aan 'n probleem voor die klas werk, werk saam met die onderwyser deur aan die probleem in u notaboek te werk.
- Maak seker dat u aantekeninge duidelik en maklik leesbaar is. Moenie net vrae skryf nie. Skryf ook alles neer wat die onderwyser sê wat u begrip van die begrippe wat verduidelik word, kan verbeter.
- Voltooi die voorbeeldvrae wat u onderwyser gegee het. Terwyl die onderwyser in die klas rondloop terwyl u werk, beantwoord die vrae wat gevra word.
- Neem deel wanneer die onderwyser 'n probleem oplos. Moenie wag dat die onderwyser jou bel nie. Bied aan om te antwoord as u die antwoord ken, en steek u hand op om 'n vraag te stel as u nie seker is van die materiaal wat geleer word nie.

Stap 3. Doen u huiswerk op dieselfde dag as u huiswerk gegee word
As u op dieselfde dag u huiswerk doen, is die konsep nog steeds vars in u gedagtes. Soms is dit nie moontlik om u huiswerk op dieselfde dag af te handel nie. Maak seker dat u huiswerk klaar is voordat u klas toe gaan.

Stap 4. Werk buite die klas as u hulp nodig het
Besoek u onderwyser tydens pouses of gedurende kantoorure.
- As u 'n wiskundesentrum by u skool het, vind die openingstye daarvan uit en vra hulp.
- Sluit aan by 'n studiegroep. 'N Goeie studiegroep bestaan oor die algemeen uit 4 of 5 mense met verskillende vlakke. As u 'n C -student in Wiskunde is, sluit aan by 'n groep van 2 of 3 studente met 'n 'A' of 'B' graad, sodat u u vaardighede kan verbeter. Vermy om by 'n groep studente aan te sluit wie se grade laer is as joune.
Deel 2 van 6: Wiskunde leer op skool

Stap 1. Begin met rekenkunde
In die meeste skole leer studente rekenkunde op laerskool. Rekenkunde dek die basiese beginsels van optelling, aftrekking, vermenigvuldiging en deling.
- Doen oefenvrae. Om rekenkundige probleme oor en oor te doen, is die beste manier om die basiese beginsels korrek te memoriseer. Soek sagteware waarmee u 'n wye verskeidenheid verskillende wiskundige probleme kan werk om mee te werk. Soek ook probleme met tydsraamwerke om u spoed te verbeter.
- U kan ook rekenkundige probleme aanlyn vind, en u kan rekenkundige programme op u mobiele toestel aflaai.

Stap 2. Gaan voort met die pre-algebra
Hierdie oefening gee u die basiese elemente wat u nodig het om algebra -probleme later op te los.
- Leer meer oor breuke en desimale. U leer breuke en desimale optel, aftrek, vermenigvuldig en deel. Wat breuke betref, leer u hoe om breuke af te trek en gekombineerde getalle te vertaal. Wat desimale betref, sal u plekwaardes verstaan, en u kan desimale in storieprobleme gebruik.
- Lees meer oor verhoudings, verhoudings en persentasies. Hierdie konsepte sal u help om vergelykings te tref.
- Stel jouself voor aan basiese meetkunde. U leer 3D -vorms en -konsepte. U leer ook konsepte soos oppervlakte, omtrek, volume en oppervlakte, asook inligting oor parallelle en loodregte lyne en hoeke.
- Verstaan 'n paar basiese statistieke. In die pre-algebra bevat u inleiding tot statistiek oor die algemeen beeldmateriaal soos grafieke, spreidingsgrafieke, seëlgrafieke en histogramme.
- Leer die basiese beginsels van algebra. Dit sluit konsepte in soos die oplossing van eenvoudige vergelykings wat veranderlikes bevat, leer oor eienskappe soos die verspreidingseiendom, eenvoudige vergelykings teken en ongelykhede oplos.
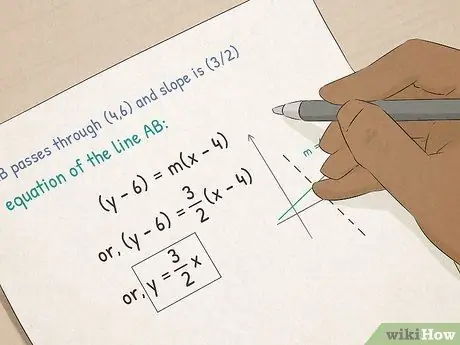
Stap 3. Gaan na Algebra I
In u eerste jaar van algebra leer u meer oor die basiese simbole wat in algebra ingesluit is. U sal ook leer om:
- Los vergelykings en ongelykhede wat veranderlikes bevat, op. U sal leer hoe om hierdie probleme op papier op te los en hoe u dit met foto's kan oplos.
- Los storieprobleme op. U sal verbaas wees hoeveel daaglikse probleme u in die toekoms sal ondervind, wat die vermoë vereis om algebraïese storieprobleme op te los. U sal byvoorbeeld algebra gebruik om uit te vind watter rentekoers u op u bankrekening of belegging verdien. U kan ook algebra gebruik om uit te vind hoe lank u moet ry op grond van die snelheid van u motor.
- Werk met eksponente. As u begin om polinoomvergelykings op te los (uitdrukkings wat getalle en veranderlikes bevat), sal u verstaan hoe u eksponente moet gebruik. Dit sal waarskynlik oefeninge met wetenskaplike notasie insluit. Sodra u eksponente bemeester het, kan u leer om polinome uitdrukkings by te voeg, af te trek, te vermenigvuldig en te verdeel.
- Los vierkants- en vierkantswortelprobleme op. As u hierdie onderwerp onder die knie kry, kan u die vierkante van baie getalle memoriseer. U sal ook met vergelykings met vierkantswortels kan werk.
- Verstaan funksies en grafieke. In algebra leer u grafiese vergelykings. Jy sal leer hoe om die helling van 'n lyn te bereken, hoe om 'n vergelyking in 'n punt-hellingvorm te plaas, en hoe om die x-en-y-sny van 'n lyn te bereken met behulp van die helling-afsnitvorm.
- Vind uit die stelsel van vergelykings. Soms kry u 2 verskillende vergelykings met die veranderlikes x en y, en u moet oplos vir x of y vir beide vergelykings. Gelukkig leer u baie truuks om hierdie vergelykings op te los, insluitend grafiek, vervanging en byvoeging.

Stap 4. Bestudeer meetkunde
In meetkunde leer u die eienskappe van lyne, segmente, hoeke en vorms.
- U sal 'n aantal stellings en ooreenkomste memoriseer wat u sal help om die reëls van meetkunde te verstaan.
- U sal leer hoe om die oppervlakte van 'n sirkel te bereken, hoe u die stelling van Pythagoras kan gebruik en hoe u die verhouding tussen die hoeke en sye van 'n spesiale driehoek kan vind.
- U sal baie meetkundevrae sien in toekomstige gestandaardiseerde toetse, soos die SAT, ACT en GRE.
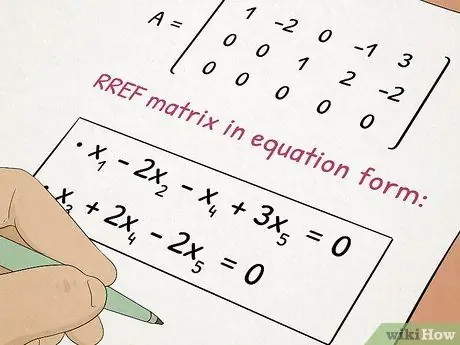
Stap 5. Neem die Algebra II -klas
Algebra II bou voort op die konsepte wat u in Algebra I geleer het, en voeg by tot komplekse onderwerpe soos kwadratiese vergelykings en matrikse.
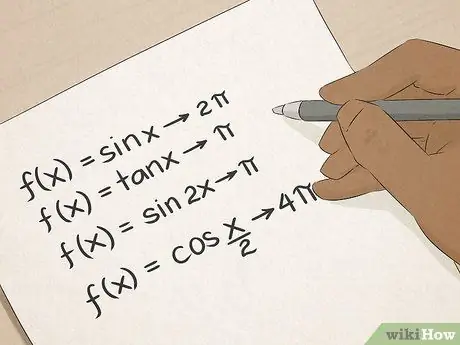
Stap 6. Bemeester trigonometrie
U ken trigonometriese terme: sinus, cosinus, raaklyn, ensovoorts. Trigonometrie leer u baie praktiese maniere om hoeke en lynlengtes te bereken, en hierdie vaardighede is van onskatbare waarde vir mense wat in konstruksie, argitektuur, ingenieurswese of landmeting werk.
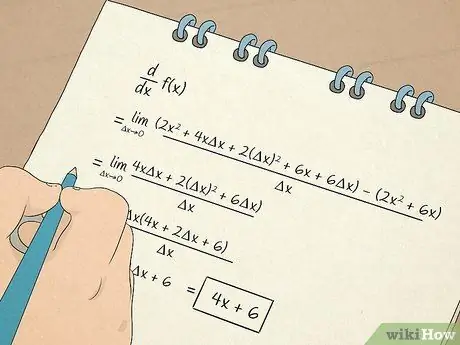
Stap 7. Voer berekeninge uit
Calculus klink dalk intimiderend, maar dit is 'n wonderlike hulpmiddel om die gedrag van getalle of die wêreld om jou te verstaan.
- Calculus leer u funksies en perke. U sal die getalgedrag van nuttige funksies sien, insluitend e^x en logaritmiese funksies.
- U sal ook leer hoe om te bereken en met afgeleides te werk. Die eerste afgeleide gee u inligting gebaseer op die helling van die raaklyn na 'n vergelyking. 'N Afgeleide gee jou byvoorbeeld die tempo waarteen iets verander in 'n nie-lineêre situasie. Die tweede afgeleide sal u vertel of die funksie oor 'n sekere interval toeneem of afneem, sodat u die konkaviteit van 'n funksie kan bepaal.
- Integrale leer u hoe u die oppervlakte onder 'n kromme sowel as die volume daarvan kan bereken.
- Berekening op hoërskool eindig gewoonlik in rye en rye. Alhoewel studente nie baie toepassings vir stroombane sal sien nie, is stroombane belangrik vir diegene wat differensiaalvergelykings bestudeer.
Deel 3 van 6: Math Fundamentals-Master Addition

Stap 1. Begin met "+1" feite
As u 1 by 'n getal voeg, neem u die hoogste getal op die getallelyn. Byvoorbeeld, 2 + 1 = 3.
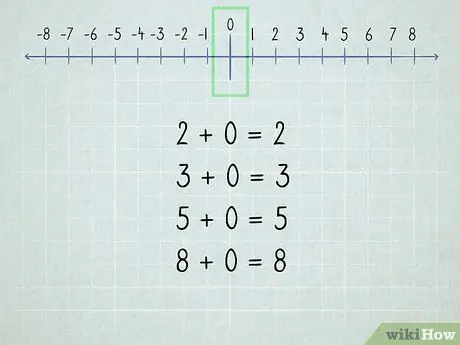
Stap 2. Verstaan die nul
Alle getalle wat by nul gevoeg word, is dieselfde getal, want "nul" beteken "geen".

Stap 3. Leer dubbele getalle
Veelvuldige getalle is 'n probleem wat die optel van twee gelyke getalle behels. Byvoorbeeld, 3 + 3 = 6 is 'n voorbeeld van 'n vergelyking met veelvuldige getalle.

Stap 4. Gebruik kartering om meer te leer oor ander opteloplossings
In die onderstaande voorbeeld leer u deur te karteer wat gebeur as u 3 tot 5, 2 en 1. byvoeg. Probeer self die 'add by 2' probleem.

Stap 5. Gaan voort totdat die getal meer as 10 is
Leer om 3 getalle bymekaar te tel om 'n getal groter as 10 te kry.
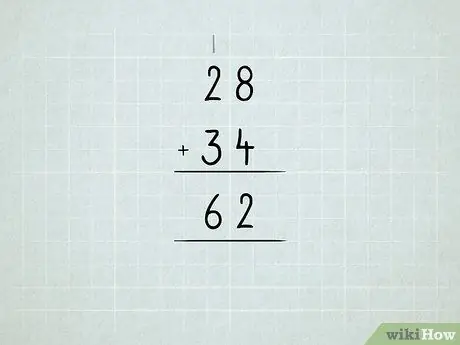
Stap 6. Tel die groter getalle op
Lees meer oor die hergroepering van eenhede in tiene, tiene in honderde, ensovoorts.
- Tel eers die getalle in die regterkolom op. 8 + 4 = 12, wat beteken dat jy 1 getal 10 en 2 getal 1. Skryf die getal 2 onder die eenheidskolom.
-
Skryf die getal 1 in die tiene kolom neer.
-
Tel die kolom tiene in sy geheel op.
Deel 4 van 6: Wiskundige grondbeginsels-verminderingstrategieë

Leer wiskunde Stap 18 Stap 1. Begin met "agteruit 1 syfer
As u 1 van 'n getal aftrek, neem u 1 getal terug. Byvoorbeeld, 4 - 1 = 3.

Leer wiskunde Stap 19 Stap 2. Leer om dubbele getalle af te trek
Byvoorbeeld, jy tel die getalle 5 + 5 by om 10. Kry net die vergelyking agteruit om 10 - 5 = 5 te kry.
- As 5 + 5 = 10, dan is 10 - 5 = 5.
-
As 2 + 2 = 4, dan is 4 - 2 = 2.

Leer wiskunde Stap 20 Stap 3. Memoriseer die feitefamilie
As 'n voorbeeld:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

Leer wiskunde Stap 21 Stap 4. Soek die ontbrekende getalle
Byvoorbeeld, _ + 1 = 6 (die antwoord is 5).

Leer wiskunde Stap 22 Stap 5. Memoriseer die feit van aftrekking tot 20

Leer wiskunde Stap 23 Stap 6. Oefen om 1-syfergetalle van 2-syfergetalle af te trek sonder om te leen
Trek die getalle in die ene kolom af en verminder die getalle in die tiene kolom.
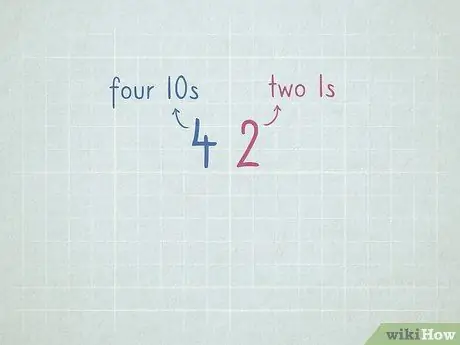
Leer wiskunde Stap 24 Stap 7. Oefen plekwaarde om voor te berei op aftrekking deur te leen
- 32 = 3 getalle 10 en 2 getalle 1.
- 64 = 6 getalle 10 en 4 getalle 1.
- 96 = _ nommer 10 en _ nommer 1.
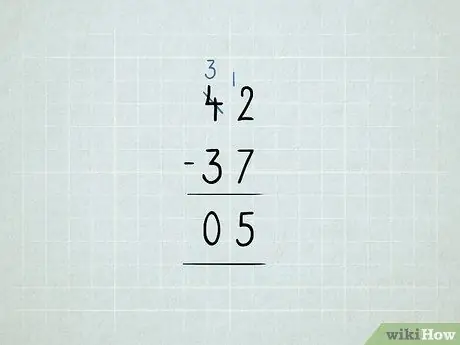
Leer wiskunde Stap 25 Stap 8. Trek af deur te leen
- U wil 42 - 37 aftrek. U begin deur 2 - 7 in die eenheidskolom af te trek. Dit blyk dat dit nie gewerk het nie!
-
Leen die getal 10 uit die tiene kolom en plaas dit in die kolom. Nou het jy 3 10's in plaas van 4 10. Nou het jy 12 1's in plaas van 2 1's.
-
Trek eers die eenheidskolom af: 12 - 7 = 5. Kontroleer dan die tiene kolom. Aangesien 3 - 3 = 0, hoef u nie die getal 0. neer te skryf nie. U antwoord is 5.
Deel 5 van 6: Wiskundebeginsels-Meestervermenigvuldiging

Leer wiskunde Stap 26 Stap 1. Begin met die getal 1 en die getal 0
Alle getalle wat met 1 vermenigvuldig word, is dieselfde as die getal self. Enige getal vermenigvuldig met 0 is gelyk aan nul.

Leer wiskunde Stap 27 Stap 2. Memoriseer die vermenigvuldigingstabel

Leer wiskunde Stap 28 Stap 3. Oefen met enkele syfers vermenigvuldigingsprobleme

Leer wiskunde Stap 29 Stap 4. Vermenigvuldig die 2-syfergetal met die 1-syfergetal
- Vermenigvuldig die nommer regs onder met die nommer regs bo.
-
Vermenigvuldig die nommer regs onder met die nommer links bo.
Leer wiskunde Stap 30 Stap 5. Vermenigvuldig 2 2-syfergetalle
- Vermenigvuldig die nommer regs onder met die nommer regs bo en dan met die nommer links bo.
-
Beweeg die tweede ry een syfer na links.
- Vermenigvuldig die nommer links onder met die nommer regs bo en dan die nommer links bo.
-
Voeg al die kolomme by.
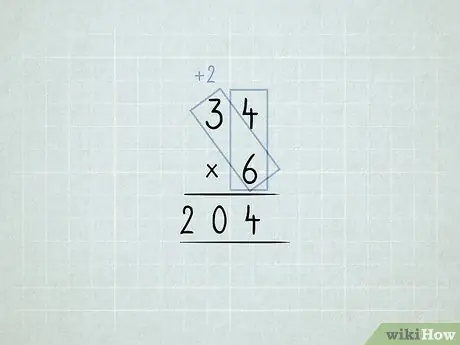
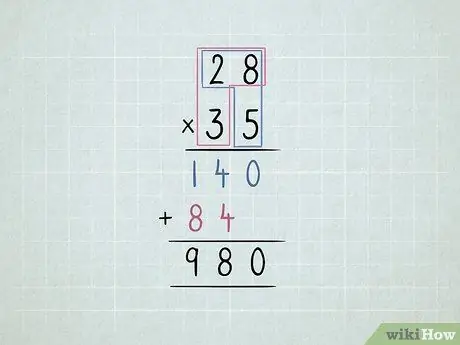
Leer wiskunde Stap 31 Stap 6. Vermenigvuldig en hergroepeer die kolomme
- U wil 34 x 6 vermenigvuldig. U begin deur die eenheidskolom (4 x 6) te vermenigvuldig, maar u kan nie 24 1s in die een -kolom hê nie.
-
Stoor 4 1'e in die eenheidskolom. Beweeg 2 10s na die tiene kolom.
-
Vermenigvuldig 6 x 3, wat gelyk is aan 18. Voeg die 2 by wat jy beweeg het, wat gelyk is aan 20.
Deel 6 van 6: Wiskundige grondbeginsels-onthul afdelingsprobleme

Leer wiskunde Stap 32 Stap 1. Dink aan deling in teenstelling met vermenigvuldiging
#* As 4 x 4 = 16, dan 16 /4 = 4.
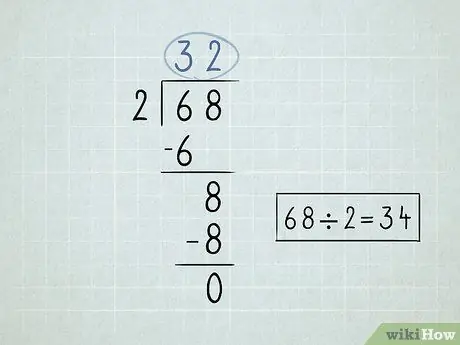
Leer wiskunde Stap 33 Stap 2. Skryf jou delingsprobleem neer
- Verdeel die getal links van die verdelingsimbool, of verdeler, met die eerste getal onder die verdelersimbool. Aangesien 6 /2 = 3, skryf u die getal 3 bo die divisiesimbool.
-
Vermenigvuldig die getal bo die delingsimbool met die deler. Bring die resultaat onderaan die eerste getal onder die afdeling simbool. Aangesien 3 x 2 = 6, dan verlaag u die getal 6.
- Trek die 2 getalle wat u neergeskryf het, af. 6 - 6 = 0. U kan 0 leeg laat, omdat u gewoonlik nie getalle met 0 begin nie.
-
Verlaag die tweede getal wat onder die divisiesimbool is.
- Verdeel die getal wat jy afbring deur die verdeler. In hierdie geval, 8 /2 = 4. Skryf die getal 4 bo die delingsimbool neer.
-
Vermenigvuldig die boonste regtergetal met die deler en bring die getal af. 4 x 2 = 8.
-
Trek die getalle af. Die finale aftrekking gee nul, wat beteken dat u die probleem opgelos het. 68 x 2 = 34.

Leer wiskunde Stap 34 Stap 3. Bereken ook die res
Sommige van die verdelers is nie volledig in ander getalle verdeel nie. As u die laaste aftrekking voltooi het en u nie meer getalle hoef te aflei nie, dan is die laaste getal die res.






