Solank jy die maat van die ander twee hoeke ken, is dit maklik om die derde hoek van 'n driehoek te vind. U hoef net die som van die twee hoeke met 180 grade af te trek. Daar is egter ook ander maniere waarop u die derde hoek van 'n driehoek kan vind as die probleem 'n bietjie anders is as gewoonlik. As u wil weet hoe u die derde hoek van 'n driehoek kan vind, volg die onderstaande gids.
Stap
Metode 1 van 3: Die metings van die ander twee hoeke gebruik
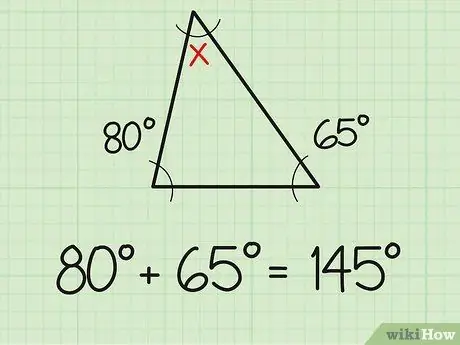
Stap 1. Tel die twee bekende hoeke bymekaar
Een feit wat u moet weet, is dat die som van die drie hoeke van 'n driehoek altyd 180 grade is. As u dus reeds die mate van die twee hoeke van 'n driehoek ken, is die vind van die derde hoek net so eenvoudig as om eenvoudige optel- en aftrekprobleme te doen. Tel eers die twee hoekmetings by wat u reeds ken. Twee bekende hoeke meet byvoorbeeld 80 en 65 grade. Voeg die twee bymekaar (80+65), en u kry 145 grade.
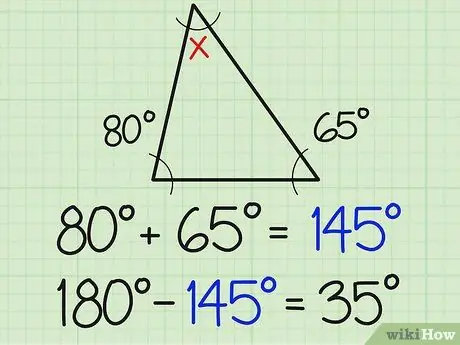
Stap 2. Verdeel die getal met 180
Die som van die drie hoeke van 'n driehoek is altyd 180 grade. Daarom moet die derde hoek 180 wees wanneer dit bygevoeg word tot die som van die twee bekende metings van die hoek. In die voorbeeld hierbo beteken dit 180-154 = 35.
Stap 3. Skryf jou antwoord neer
Nou het u die antwoord op die derde hoek (in die voorbeeld 35 grade). As u nog steeds twyfel, kyk self. Voeg die drie hoeke bymekaar en jy kry 'n resultaat van 180. As jy dit nie doen nie, is jou berekening verkeerd. Vir hierdie voorbeeld, 80+65+35 = 180. As dit korrek is, beteken dit dat u die probleem opgelos het.
Metode 2 van 3: Die gebruik van veranderlikes
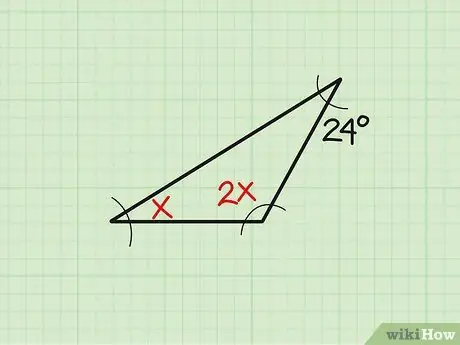
Stap 1. Skryf die probleem neer
Soms word die grootte van die bestaande hoek in 'n veranderlike vorm getoon. Kom ons neem hierdie voorbeeld: "Vind die hoek" x "van 'n driehoek as die drie hoeke onderskeidelik" x "," 2x "en 24 meet." Skryf eers die probleem neer.
Stap 2. Tel al die hoekmetings op
Die beginsel wat u moet onthou, bly dieselfde. Tel dus eers die drie hoeke in die probleem op, naamlik "x+2x+24 = 3x+24".
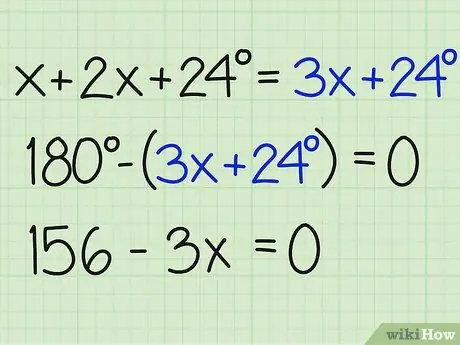
Stap 3. Deel die som van die hoeke met 180
Nou, verskil die getal met 180 grade om x te vind en vind die antwoord op die probleem. Maak seker dat u die vergelyking gelyk aan nul eindig. Hier is hoe dit geskryf is:
- 180- (3x+24) = 0
- 180-3x-24 = 0
- 156-3x = 0
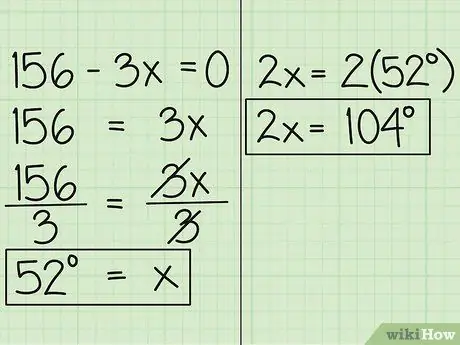
Stap 4. Vind die waarde van x
Skuif nou die veranderlike na die ander kant van die vergelyking, en u kry 156 = 3x. Deel dan die vergelyking met 3, sodat jy x = 52 kry. Dit beteken dat die hoekmaat in x uitgedruk is 52 grade. Die ander hoek, uitgedruk in 2x, is 52 grade maal 2, wat 104 grade is.
Stap 5. Gaan u resultate na
As u wil seker maak dat u antwoord korrek is, tel die drie hoekmetings waarop u die antwoord gevind het, bymekaar. As die resultaat 180 is, beteken dit dat u antwoord korrek is. Vir hierdie voorbeeld, 52+104+24 = 180.
Metode 3 van 3: Gebruik van ander metodes
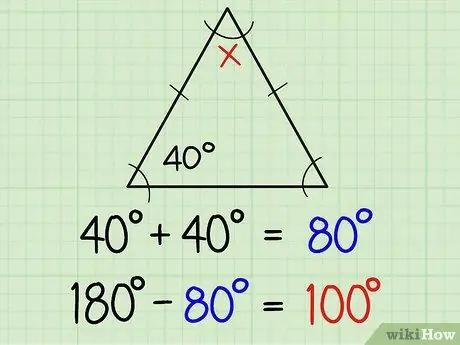
Stap 1. Vind die hoeke van 'n gelykbenige driehoek
'N Gelykbenige driehoek het twee gelyke sye en twee gelyke hoeke. Twee gelyke sye word gewoonlik gemerk met 'n klein lyn in die middel van die sylyn, wat beteken dat die twee teenoorgestelde hoeke op die lyn dieselfde maat is. As u reeds die grootte van een hoek ken, ken u outomaties die ander hoek. Hier is 'n verdere verduideliking:
As een van die gelyke hoeke 40 grade is, dan is die ander 40 grade. Op hierdie manier kan u al drie hoeke vind met die verskil tussen die som van 40+40 (dit wil sê 80) en 180, of met ander woorde 180-80 = 100
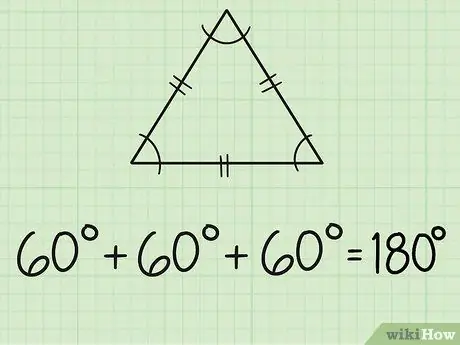
Stap 2. Vind die hoeke van 'n gelyksydige driehoek
'N Gelyksydige driehoek het drie gelyke sye en drie gelyke hoeke. Elke kant is gewoonlik gemerk met twee kort lyne in die middel. Aangesien al drie hoeke gelyk is, beteken dit dat al die hoeke 60 grade meet, want 180/3 = 60.
Stap 3. Vind die derde hoek in 'n regte driehoek
Gestel jy kry 'n regte driehoek, met een van die skerphoeke wat 30 grade meet. Aangesien die driehoek 'n regte hoek is, beteken dit dat een van die hoeke, naamlik die regte hoek, 90 grade moet meet. Gebruik dan die driehoekbeginsel, die verskil tussen die som van die twee hoeke (90+30 = 120) by 180, dan kry u 180-120 = 60 grade.
