- Outeur Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 10:50.
- Laas verander 2025-01-23 12:05.
As u dit reeds verstaan, is dit nie moeilik om gewone breuke in desimale om te skakel nie. Om gewone breuke na desimale om te skakel, kan u lang deling, vermenigvuldiging of selfs 'n sakrekenaar gebruik as u nie met die hand wil bereken nie. Sodra u die metode onder die knie het, kan u breuke maklik na desimale omskakel.
Stap
Metode 1 van 4: Met lang afdeling
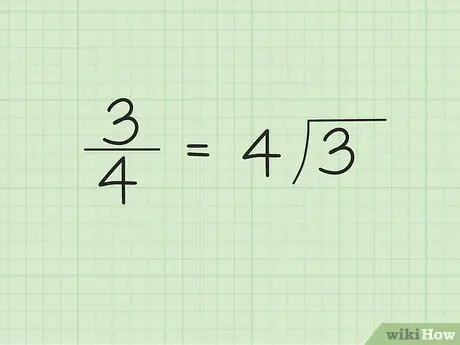
Stap 1. Skryf die noemer buite/linkerkant van die verdelersimbool en die teller binne/regterkant van die verdelersimbool neer
Gestel ons wil byvoorbeeld 3/4 na 'n desimaal omskakel. Skryf "4" buite/linkerkant van die verdelersimbool en "3" binne/regterkant van die verdelersimbool. "4" is die getal wat verdeel word en "3" is die getal wat gedeel word.

Stap 2. Skryf "0", dan 'n desimale punt ('n komma), bo die verdelersimbool
Aangesien dit 'n breuk is wat tel, moet die resultaat minder as een wees, dus hierdie stap is baie belangrik. Skryf daarna die desimale teken, dan "0", na die nommer "3" in/regterkant van die verdelersimbool. Alhoewel "3" gelyk is aan "3, 0", laat die nul toe dat "3, 0" gedeel word deur "4".

Stap 3. Bereken die antwoord met behulp van lang afdeling
Met 'n lang afdeling kan die desimale teken vir eers geïgnoreer word, sodat u slegs 30 gedeel deur 4 moet bereken.
- Verdeel eers 3, 0, wat tel as 30, met 4. Die naaste 4 tot 30 is 4 x 7 = 28, en laat 2. Skryf dus "7" na "0", bo die verdeler en "28" onder " 3, 0”in/regterkant van die verdelersimbool. Onder 28 skryf "2", die res van 30 minus 28.
- Skryf vervolgens "0" na "3, 0" sodat dit "3, 00" word, wat as "300" beskou kan word, binne/regs van die verdelersimbool. Dus kan 0 na regs van "2" verlaag word sodat "20" deelbaar is met "4".
- “20” gedeel deur “4” is gelyk aan “5”. Skryf dus "5" na "0.7" bokant die verdelersimbool sodat dit "0.75" word.

Stap 4. Skryf die finale antwoord neer
Dus, "3" gedeel deur "4" is gelyk aan "0.75". Skryf die antwoord neer. Klaar.
Metode 2 van 4: Breuke wat herhalende desimale genereer
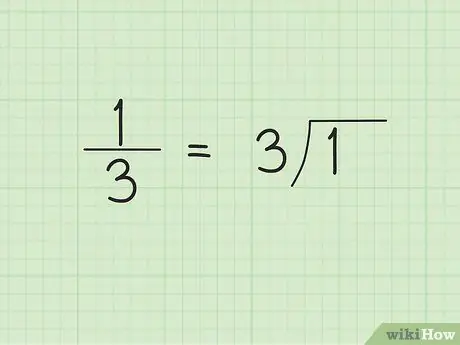
Stap 1. Maak 'n lang afdeling
As u met 'n lang-syfer-afdeling begin, kan u nie voorspel dat die resultaat 'n herhalende desimale getal sal wees nie. Gestel ons wil byvoorbeeld die gewone breuk 1/3 na desimale vorm omskakel. Skryf 3, of die noemer, aan die buitekant/linkerkant van die verdelersimbool en 1 binne/regterkant van die verdelersimbool.

Stap 2. Skryf 'n 0, dan 'n desimale teken, bo die verdelersimbool
Aangesien die resultaat minder as 1 moet wees, berei hierdie stap die antwoord voor om in desimale vorm geskryf te word. Die desimale teken moet ook regs van die getal "1" wat in/regterkant van die verdelersimbool geleë is, geskryf word.
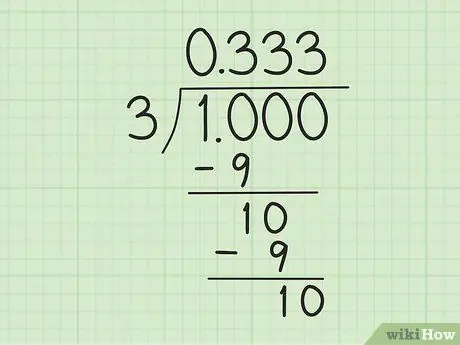
Stap 3. Begin met die berekening van lang afdeling
Begin deur "1" in "1, 0" te maak, wat tel as "10", sodat dit deelbaar is met "3". Voer vervolgens die volgende stappe uit:
- Deel 10 met 3. Gebruik 3 x 3 = 9 om 'n res van 1. te maak. Skryf dus 3 regs van die "0", bo die verdelersimbool en trek 10 by 9 af om 'n res van 1 te kry.
- Skryf 'n "0" regs van die getal "1" (die res van 10 minus 9 in die vorige stap) hieronder om nog 'n "10" te kry. As u weer "10" deur "3" deel, word dieselfde proses herhaal: skryf "3" regs van die eerste "3" bokant die verdelersimbool en trek die nuwe "10" deur "9" af.
- Gaan voort totdat 'n patroon gevorm word. Weet jy iets is vreemd? Hierdie verdeling kan vir ewig voortduur. 10 is altyd deelbaar met 3: daar sal altyd 'n "1" aan die onderkant en 'n nuwe "3" na die desimaal bo die verdelersimbool wees.
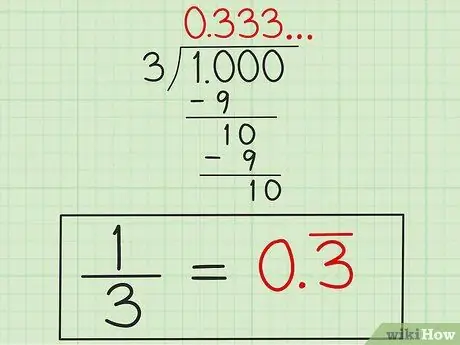
Stap 4. Skryf die antwoord neer
Nadat u geweet het dat "3" homself sal herhaal, skryf die antwoord as "0, 3" met 'n reël bo die getal "3" (of "0, 33" met 'n reël bo albei getalle "3") as 'n aanduiding dat die nommer "3" word dit steeds herhaal. Hierdie antwoord is in die desimale vorm 1/3 omdat 1 gedeel deur 3 nie vanself sal eindig nie.
Daar is baie breuke wat herhalende desimale lewer, soos 2/9 ("0, 2" met "2" herhaal), 5/6 ("0, 83" met "3" herhaal) of 7/9 ("0, 7”met“7”herhaal). Hierdie patroon kom altyd voor wanneer die noemer 'n veelvoud van 3 is en die teller nie deur die noemer deelbaar is nie
Metode 3 van 4: Deur vermenigvuldiging

Stap 1. Vind die getal wat vermenigvuldig kan word met die noemer van die breuk om 10, 100, 1000 of enige getal wat basis 10 is, te produseer
Dit kan 'n maklike manier wees om breuke in desimale om te skakel sonder om 'n lang afdeling of 'n sakrekenaar te gebruik. Soek eers 'n getal wat met die noemer van die breuk vermenigvuldig kan word om 10, 100, 1,000, ensovoorts te kry. Om dit te doen, verdeel eers 10, dan 100, dan 1000, ensovoorts deur die noemer totdat u 'n heelgetal kry. Voorbeeld:
- 3/5. 10/5 = 2.2 is 'n heelgetal. 2 kan met 5 vermenigvuldig word om 10. Dit kan dus 2 gebruik word.
- 3/4. 10/4 = 2, 5. 2, 5 is nie 'n heelgetal nie. 100/4 = 25. 25 is 'n heelgetal. 25 kan met 4 vermenigvuldig word om 100 te maak. 25 kan dus gebruik word.
- 5/16. 10/16 = 0, 625, 100/16 = 6, 25, 1,000/16 = 62, 5, 10,000/16 = 625. 625 is die eerste heelgetal wat verkry word. 625 kan met 16 vermenigvuldig word om 10 000 te kry. Dus, 625 kan gebruik word.
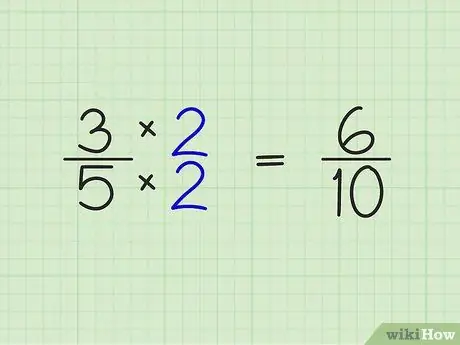
Stap 2. Vermenigvuldig die teller en noemer van die breuk met die hele getal wat uit die vorige stap verkry is
Hierdie stap is redelik maklik. Vermenigvuldig die getalle bo en onder die breuk met die hele getal wat u in die vorige stap gekry het. Voorbeeld:
- 3/5 x 2/2 = 6/10
- 3/4 x 25/25 = 75/100
- 5/16 x 625/625 = 3.125/10000

Stap 3. Skryf die finale antwoord neer
Die antwoord is dat die teller met 'n desimale gemerk is volgens die getal 0's in die noemer. Tel net hoeveel 0's in die noemer is. As daar slegs 1 0 in die noemer is, skuif die desimale punt met 1 syfer na links, ensovoorts. Voorbeeld:
- 3/5 = 6/10 = 0, 6
- 3/4 = 75/100 = 0, 75
- 5/16 = 3.125/10.000 = 0, 3125
Metode 4 van 4: Met sakrekenaar

Stap 1. Verdeel die teller deur die noemer
Hierdie metode is baie maklik. Gebruik net 'n sakrekenaar om die teller, die getal bo -aan die breuk, deur die noemer te deel, die getal onderaan die breuk. Sê byvoorbeeld dat u 3/4 na 'n desimale wil omskakel. Tik net op "3", dan op die verdelingsimbool ("÷ '"), dan op "4" en laastens die gelyke simbool ("=").

Stap 2. Skryf die antwoorde neer wat u kry
Die antwoord is 0.75. Dus, die desimale vorm van die gewone breuk 3/4 is 0.75.
Wenke
- Om te kyk of u antwoord korrek is, vermenigvuldig u die antwoord met die noemer van die breuk. As u antwoord korrek is, is die produk van die vermenigvuldiging die teller van die breuk.
- Sommige breuke kan in desimale omgeskakel word deur vergelykbare breuke te skep waarvan die noemers basis 10 is (10, 100, 1000, ensovoorts). Gebruik dan plekwaardes om die korrekte desimale vorm neer te skryf.






