Die geometriese gemiddelde is 'n ander manier om die gemiddelde waarde van 'n stel getalle te bepaal, wat gedoen word deur die waardes te vermenigvuldig voordat die wortels geneem word, in plaas van die waardes bymekaar te tel en te deel soos in 'n rekenkundige gemiddelde. Die meetkundige gemiddelde kan gebruik word om die gemiddelde opbrengskoers in finansiële analise te bereken of om die groeikoers van iets oor 'n tydperk aan te toon. Om die geometriese gemiddelde te vind, vermenigvuldig al die waardes voordat u begin, wat die totale aantal getalle in die stel is. U kan ook die logaritmefunksie in u sakrekenaar gebruik om die meetkundige gemiddelde te vind, indien u dit verkies.
Stap
Metode 1 van 2: Vind die meetkundige gemiddelde van 'n stel waardes
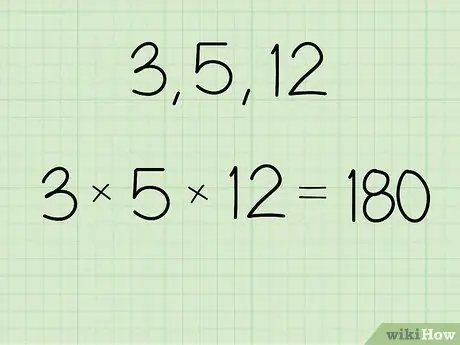
Stap 1. Vermenigvuldig die waarde waarvoor u die meetkundige gemiddelde wil vind
U kan 'n sakrekenaar gebruik of met die hand bereken om die resultaat te kry. Skryf die resultate neer sodat u dit nie vergeet nie.
- As die stel getalle byvoorbeeld 3, 5 en 12 is, bereken: (3 x 5 x 12) = 180.
- Vir 'n ander voorbeeld, as u die meetkundige gemiddelde van die stel getalle 2 en 18 wil vind, skryf: (2 x 18) = 36.
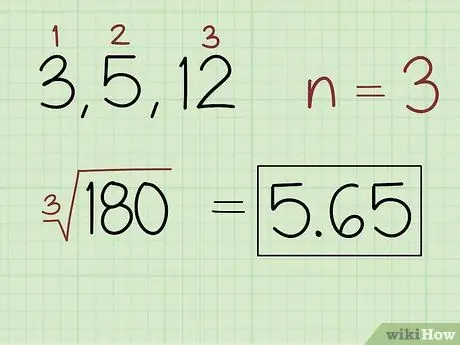
Stap 2. Vind die nde wortel van die produk, waar n die aantal waardes in die stel is
Tel die aantal getalle in die stel om die waarde te kry. Gebruik die waardes om die wortel te spesifiseer wat in die produk gebruik moet word. Gebruik byvoorbeeld die vierkantswortel as die stel 2 getalle bevat, die kubieke wortel as die stel 3 getalle bevat, ensovoorts. Gebruik 'n sakrekenaar om die vergelyking op te los en skryf die antwoord neer.
- Byvoorbeeld, vir 'n stel getalle 3, 5 en 12, skryf: (180) 5, 65.
- In die tweede voorbeeld met die stel wat 2 en 18 bevat, skryf: (36) = 6.
Variasie:
U kan ook die wortel as die eksponent van 1/ skryf as dit makliker is om dit op 'n sakrekenaar te skryf. Byvoorbeeld, vir die stel getalle 3, 5 en 12, skryf (180)1/3 in plaas van (180).
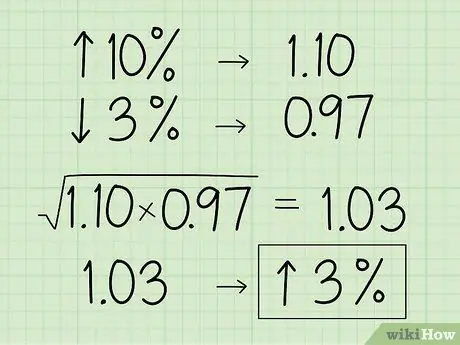
Stap 3. Skakel die persentasie om na sy desimale vermenigvuldiger -ekwivalent
As die stel getalle as 'n toename of afname in persentasie geskryf word, probeer om nie die persentasiewaarde in die meetkundige gemiddelde te gebruik nie, want die resultate sal nie akkuraat wees nie. As die persentasie toeneem, skuif die desimale punt twee syfers na links en tel 1. As die persentasie afneem, skuif die desimale punt 2 syfers na links en trek af van 1.
- Sê byvoorbeeld dat u die geometriese gemiddelde van objekwaardes wil vind wat met 10%toeneem en dan met 3%afneem.
- Skakel 10% om na 'n desimale getal en tel 1 by om 1, 10 te kry.
- Skakel dan 3% om na 'n desimale getal en trek 1 af om 0,97 te kry.
- Gebruik albei desimale plekke om die meetkundige gemiddelde te vind: (1, 10 x 0.97) 1.03.
- Skakel die getal terug na 'n persentasie deur die desimale punt met 2 syfers na regs te skuif en 1 af te trek om 'n styging van 3% in waarde te kry.
Metode 2 van 2: Berekening van die meetkundige gemiddelde met behulp van logaritmes
Stap 1. Tel die logaritmiese waardes vir elke getal in die stel op
Die LOG -funksie in die sakrekenaar neem die basis 10 van 'n getal en bepaal hoeveel u met 10 moet vermenigvuldig sodat dit gelyk is aan die getal. Soek die LOG -funksie op die sakrekenaar, wat gewoonlik aan die linkerkant van die knoppie is. Klik op die LOG -knoppie en voer die eerste nommer in die stel in. Tik “+” voordat u LOG vir die tweede nommer invoer. Gaan voort om die LOG -funksie vir elke getal met 'n plus -simbool te skei voordat u die som kry.
- Byvoorbeeld, vir stelle 7, 9 en 12, tik log (7) + log (9) + log (12), en druk dan "=" op die sakrekenaar. As die funksie bereken is, sal die getal ongeveer 2.878521796 wees.
- U kan ook elke logaritme afsonderlik bereken voordat u dit bymekaar tel.
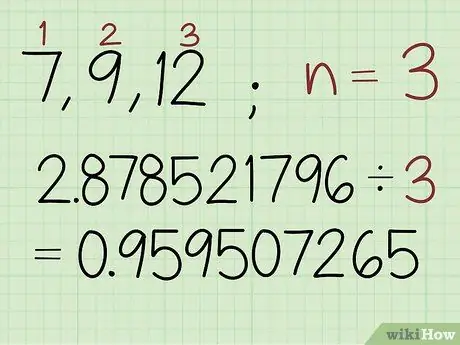
Stap 2. Verdeel die som van die logaritmiese waardes deur die aantal getalle in die stel
Tel die aantal waardes in die stel en deel die getal wat voorheen verkry is deur die getal. Die resultaat is die logaritme van die meetkundige gemiddelde.
In hierdie voorbeeld is daar 3 getalle in die stel, tik dus: 2, 878521796 /3 0, 959507265
Stap 3. Soek die antilog van die kwosiënt om die meetkundige gemiddelde te bepaal
Die antilog -funksie is die omgekeerde van die LOG -funksie op die sakrekenaar en skakel die waarde terug na basis 10. Soek die simbool "10x”Op die sakrekenaar, wat gewoonlik 'n sekondêre funksie van die LOG -knoppie is. Druk die "2de" knoppie in die linker boonste hoek van die sakrekenaar, gevolg deur die LOG knoppie om antilog te aktiveer. Voer die kwosiënt in die laaste stap in voordat die vergelyking opgelos word.
In hierdie voorbeeld sal die sakrekenaar die volgende vertoon: 10(0, 959507265) ≈ 9, 11.
Wenke
- U kan nie die meetkundige gemiddelde van negatiewe getalle vind nie.
- Alle stelle met 0 sal 'n meetkundige gemiddelde van 0 hê.
