Met die rangkorrelasiekoëffisiënt van Spearman kan ons identifiseer of twee veranderlikes 'n monotoniese funksieverhouding het (dit wil sê, as een getal toeneem, sal die ander getal ook toeneem, of andersom). Om die rangkorrelasiekoëffisiënt van Spearman te bereken, moet u datastelle rangskik en vergelyk om d te vind2, en voer dan die data in die standaard of vereenvoudigde Spearman -rangkorrelasiekoëffisiëntformule in. U kan hierdie koëffisiënte ook bereken met behulp van Excel -formules of die R -opdrag.
Stap
Metode 1 van 3: Handmatige manier
Stap 1. Skep 'n tabel
Die tabel word gebruik om al die inligting in te sluit wat nodig is om die Spearman -rangkorrelasiekoëffisiënt te bereken. U benodig 'n tafel soos hierdie:
- Skep 6 kolomme met opskrifte, soos in die voorbeeld.
- Berei soveel leë rye voor as die aantal datapare.
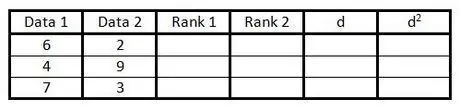
Stap 2. Vul die eerste twee kolomme in met datapare
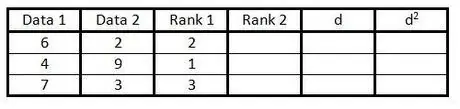
Stap 3. Voer die posisie van die eerste kolom van datagroepe in die derde kolom in van 1 tot n (aantal data)
Gee 'n gradering van 1 vir die laagste waarde, 'n telling van 2 vir die volgende laagste waarde, ensovoorts.
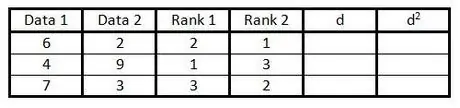
Stap 4. In die vierde kolom, doen dieselfde as in stap 3, maar om die data in die tweede kolom te rangskik
-
Gemiddeld_742 As daar twee (of meer) data is wat dieselfde waarde het, bereken die gemiddelde gradering van die data en voer dit dan in 'n tabel op wat gebaseer is op hierdie gemiddelde waarde.
In die voorbeeld regs is daar twee waardes van 5 op die graderings 2 en 3. Aangesien daar twee 5's is, vind die gemiddelde van die graderings. Die gemiddelde van 2 en 3 is 2,5, dus voer 'n beoordelingswaarde van 2,5 vir beide waardes 5 in.
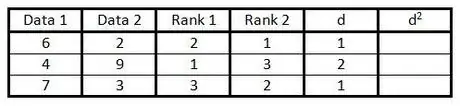
Stap 5. Bereken in kolom "d" die verskil tussen die twee getalle in die rangkolom
Dit wil sê, as een kolom 1 is en die ander kolom 3, is die verskil 2. (Die teken maak nie saak nie, want die volgende stap is om die waarde te vierkantig.)
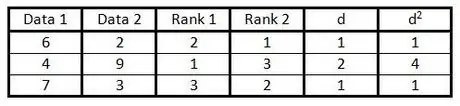
Stap 6. Vierkant elke getal in kolom "d" en skryf die resultaat in kolom "d2".
Stap 7. Voeg alle data in kolom d2".
Die resultaat is d2.
Stap 8. Kies een van die volgende formules:
-
As nie een van die graderings dieselfde is as in die vorige stap nie, voer hierdie waarde in die vereenvoudigde formule van die korrelasiekoëffisiënt van Spearman Rank in
Stap 8_271 en vervang "n" met die aantal datapare om die resultaat te kry.
Stap 9_402 -
As daar 'n soortgelyke rang in die vorige stap is, gebruik die standaard formule van die Spearman -rangkorrelasiekoëffisiënt:
Spearman
Stap 9. Interpreteer die resultate
Die waarde kan wissel tussen -1 en 1.
- As die waarde naby -1 is, is die korrelasie negatief.
- As die waarde naby 0 is, is daar geen lineêre korrelasie nie.
- As die waarde naby 1 is, is die korrelasie positief.
Metode 2 van 3: Gebruik Excel
Stap 1. Skep 'n nuwe kolom vir die data saam met die posisie daarvan
As u data byvoorbeeld in kolom A2: A11 is, gebruik die formule "= RANK (A2, A $ 2: A $ 11)" en kopieer dit totdat dit al die kolomme en rye dek.
Stap 2. Verander dieselfde gradering as beskryf in stap 3 en 4 van metode 1
Stap 3. Bereken in die nuwe sel die korrelasie tussen die twee rangkolomme met die formule "= CORREL (C2: C11, D2: D11)"
In hierdie voorbeeld verwys C en D na die kolom waar die posisie geleë is. Die nuwe sel word gevul met die Spearman Rank -korrelasie.
Metode 3 van 3: Gebruik R
Stap 1. Installeer eers die R -program as u dit nog nie het nie
(Sien
Stap 2. Stoor u data in CSV -vorm, plaas die data wat u wil vind, in die eerste twee kolomme
Ons kan dit doen deur die menu "Stoor as" te gebruik.
Stap 3. Maak R Editor oop
As u vanaf die terminale werk, voer dan net R. As u vanaf die tafelblad werk, klik op die ikoon R.
Stap 4. Tik die volgende opdrag:
- d <- read.csv ("NAME_OF_YOUR_CSV.csv") en druk Enter.
- rolverdeling (rang (d [, 1]), rang (d [, 2]))
Wenke
Die data moet uit ten minste 5 pare bestaan, sodat die neiging gesien kan word (die aantal data is 3 pare in die voorbeeld slegs om berekeninge te vereenvoudig.)
Waarskuwing
- Die korrelasiekoëffisiënt van die Spearman -rang identifiseer slegs die sterkte van die korrelasie waar die data konsekwent styg of daal. As daar 'n ander neiging in die data is, is die rangkorrelasie van Spearman geen sal 'n akkurate voorstelling gee.
- Hierdie formule is gebaseer op die aanname dat daar geen gelyke graderings is nie. As daar dieselfde rang is as in die voorbeeld, moet ons hierdie definisie gebruik: die korrelasiekoëffisiënt van die vermenigvuldigingmoment per rang.
