- Outeur Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Laas verander 2025-01-23 12:05.
Die desimale (basis tien) getallestelsel het tien moontlike waardes (0, 1, 2, 3, 4, 5, 6, 7, 8 of 9) vir elke getalposisie. Daarteenoor het die binêre (basis twee) getallestelsel slegs twee moontlike waardes verteenwoordig deur 0 en 1 vir elke getalposisie. Aangesien die binêre getallestelsel die interne taal van elektroniese rekenaars is, weet ernstige rekenaarprogrammeerders hoe om van die desimale na die binêre getallestelsel om te skakel. Volg hierdie maklike stappe en ook hoe u hierdie omskakeling bemeester.
Stap
Metode 1 van 2: Kort afdeling deur twee met res

Stap 1. Bepaal die probleem
In hierdie voorbeeld, laat ons die desimale getal 156 omskakel10 wees 'n binêre getal. Skryf die desimale getal as die getal wat verdeel moet word in die omgekeerde delingsimbool. Skryf die basis van die bestemmingsgetallestelsel (in hierdie voorbeeld "2" vir binêre) as die buite-kromme deler van die delingsimbool.
- Hierdie metode is baie makliker om te verstaan as dit op papier geteken word, en baie makliker vir beginners, omdat dit slegs deur twee deel.
- Om verwarring voor en na omskakeling te voorkom, skryf die basisnommer van die getallestelsel wat u bereken as 'n subskripsie (kleinletters onder normale letters as 'n onderskeidende teken) vir elke getal neer. In hierdie voorbeeld het die desimale getal 'n subskripsie van 10 en die binêre getal 'n subskripsie van 2.

Stap 2. Doen die verdeling
Skryf die heelgetalantwoord (kwosiënt) onder die langafdelingsimbool en skryf die res (0 of 1) regs van die gedeelde getal.
Omdat ons deur twee deel, as die getal wat gedeel word 'n ewe getal is, dan is die res 0, en as die getal wat gedeel word 'n onewe getal is, dan is die res 1

Stap 3. Gaan voort om te deel totdat dit nul bereik
Gaan afdraande, deel elke nuwe kwosiënt met twee en skryf die res aan die regterkant van elke gedeelde getal. Stop wanneer die kwosiënt nul is.

Stap 4. Skryf die nuwe binêre getal neer
Lees vanaf die laagste getal wat oorbly, die volgorde van die res in stygende volgorde na bo. In hierdie voorbeeld moet u die resultaat 10011100 kry. Dit is die binêre ekwivalent van die desimale getal 156. Of, as dit met sy numeriese basis -subskripsie geskryf is: 15610 = 100111002.
Hierdie metode kan aangepas word om van desimale basis na enige getalbasis om te skakel. Die verdeler is 2 omdat die basis van die bestemmingsgetalstelsel basis 2 (binêre) is. As die basis van die bestemmingsgetalstelsel 'n ander basis is, vervang die basis 2 -nommer in hierdie metode met die toepaslike basisnommer. Byvoorbeeld, as die bestemmingsbasis basis 9 is, vervang die basis 2 -nommer met 9. Die finale uitslag sal direk in die vorm van die bestemmingsbasisnommer wees
Metode 2 van 2: afleiding van krag van twee en aftrekking

Stap 1. Begin deur 'n tabel te skep
Skryf die kragte van die twee basisgetalle in die "tabel 2 -basis" van regs na links neer. Begin by 20, skryf dit as "1". Verhoog die rang met 1 vir elke rang. Voltooi die tabel totdat u 'n getal kry wat die naaste aan die nommer van die desimale getallestelsel is wat u bereken. In hierdie voorbeeld, laat ons die desimale getal 156 omskakel10 wees 'n binêre getal.

Stap 2. Vind die getal met die grootste krag van die basisgetal 2
Kies in die tabel die grootste getal wat gelyk is aan of minder is as die getal wat omgeskakel moet word. Die getal 128 is die getal met die grootste krag van die basisgetal 2 en is ook kleiner as 156, so skryf 'n getal "1" onder hierdie blokkie in die tabel, waar die grootste getal uit die tabel aan die linkerkant is (sien tabel in die prent hierbo). Trek dan 128 van die aanvanklike getal af, u kry: 156 - 128 = 28.
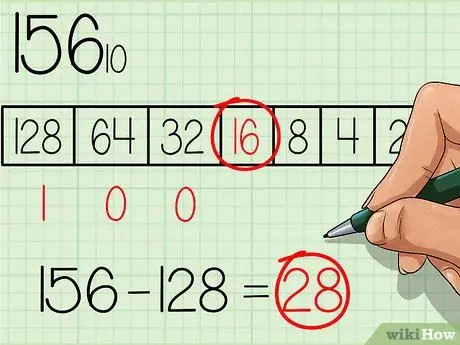
Stap 3. Gaan na die volgende kleiner krag in die tabel
Gebruik die nuwe nommer (28) en gaan deur die tabel van links na regs terwyl u kyk of die getalle gelyk is aan of minder is as die nuwe getal. Die getal 64 is nie minder nie as 28, so skryf die getal “0” onder die getalvak 64. Gaan voort totdat u 'n getal kry wat gelyk is aan of minder as 28.
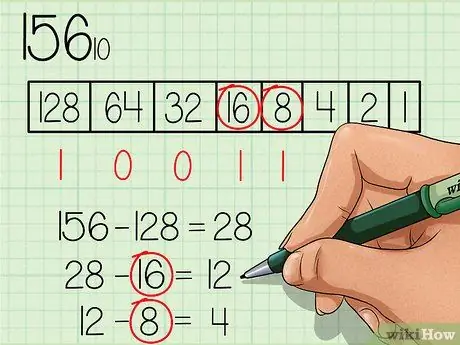
Stap 4. Trek elke getal wat gelykstaande is aan of kleiner as die nuwe getal af is, af en merk die getal "1" onder die blokkie vir die toepaslike getal
Die getal 16 is minder as 28, so skryf die getal "1" onder die getalbus 16 en trek 16 af van 28, sodat u 'n nuwe getal 12. kry. Die getal 8 is minder as 12, so skryf die getal "1" onder die getalbus 8 en trek 8 van 12 af om die nuwe getal 4 te kry.

Stap 5. Gaan voort totdat u aan die einde van die tafel kom
Onthou om 'n "1" onder elke blokkie te merk vir getalle wat gelyk is aan of kleiner is as die nuwe getal, en 'n "0" onder elke blokkie vir getalle wat nog groter is as die nuwe getal.
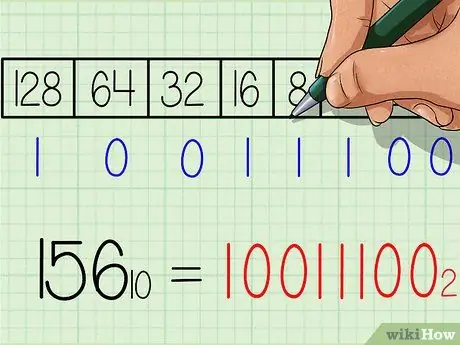
Stap 6. Skryf die antwoord vir die binêre getal neer
Die getal sal presies dieselfde wees van links na regs as die ry met syfers "1" en "0" onderaan die tabel. U moet die resultaat 10011100 kry. Dit is die binêre ekwivalent van die desimale getal 156. Of as dit met 'n onderskrif geskryf is: 15610 = 100111002.
Deur hierdie metode te herhaal, kan u die kragte van die tweede basis onthou, sodat u stap 1 kan oorslaan
Wenke
- Die sakrekenaarprogram wat in die bedryfstelsel ingebou is, kan hierdie omskakeling vir u doen, maar as programmeerder is dit die beste om te begin met 'n goeie begrip van hoe omskakelings werk. Die omskakelingsopsies in die sakrekenaarprogram kan sigbaar gemaak word deur die menu "View" oop te maak en "Programmer" te kies (vir Windows 7 en 8).
- Omskakel in die teenoorgestelde rigting, dit wil sê van die binêre na desimale getallestelsel, is gewoonlik makliker om eers te leer.
- Oefen gereeld om desimale getalle in binêre om te skakel om meer kundig te word.






